簡介
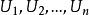 ε覆蓋
ε覆蓋 設 X 是巴拿赫空間,x∈X,‖x‖表示 x 的範數,A 是X的緊子集,ε>0 是給定的正數,如果是 X 的一族子集,每個 U的直徑都不超過 2ε,亦即
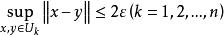 ε覆蓋
ε覆蓋 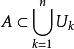 ε覆蓋
ε覆蓋 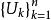 ε覆蓋
ε覆蓋 而且那么稱集族是A的一個ε覆蓋。
推廣
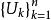 ε覆蓋
ε覆蓋 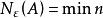 ε覆蓋
ε覆蓋 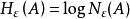 ε覆蓋
ε覆蓋 對於給定的ε> 0,A的ε覆蓋中集U的個數n是與這個集族的選取有關的,但n的最小值卻是一個僅與ε有關的關於集A的不變數,即當A給定後,N(A)是一個僅與ε有關的非負整數,人們稱數為集A的熵,或者區別於機率論中的同名概念,稱H(A)為集A的度量熵。
ε網
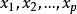 ε覆蓋
ε覆蓋 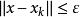 ε覆蓋
ε覆蓋 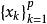 ε覆蓋
ε覆蓋 設X是巴拿赫空間,A是X的緊子集,ε>0是給定的正數,如果X中存在有限個點,使得對於每個點x∈A,都至少有x使得,也即x與x的距離ρ(x,x)不超過ε:ρ(x,xx)≤ε,則稱集為A的一個ε網。
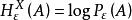 ε覆蓋
ε覆蓋 集A的ε網中點的個數p在ε>0給定後,自然與這些點的取法有關。但是p的最小值P(A) = min p卻是集A的一個不變數。它當然與空間X有關,稱數為A關於X的熵。
