Z檢驗的步驟
第一步:建立虛無假設,即先假定兩個平均數之間沒有顯著差異。
第二步:計算統計量Z值,對於不同類型的問題選用不同的統計量計算方法。
1、如果檢驗一個樣本平均數u 與一個已知的總體平均數(μ0)的差異是否顯著。其Z值計算公式為:
其中:
u 是檢驗樣本的平均數;
μ0是已知總體的平均數;
S是樣本的方差;
n是樣本容量。
2、如果檢驗來自兩個的兩組樣本平均數的差異性,從而判斷它們各自代表的總體的差異是否顯著。其Z值計算公式為:
其中:
是樣本1,樣本2的平均數;
S1,S2是樣本1,樣本2的標準差;
n1,n2是樣本1,樣本2的容量。
第三步:比較計算所得Z值與理論Z值,推斷髮生的機率,依據Z值與差異顯著性關係表作出判斷。如下表所示:
第四步:根據是以上分析,結合具體情況,作出結論。
舉例
[編輯]Z檢驗舉例
某項教育技術實驗,對實驗組和控制組的前測和後測的數據分別如下表所示,比較兩組前測和後測是否存在差異。
實驗組和控制組的前測和後測數據表
前測 實驗組 n1 = 50 S1a = 14
控制組 n2 = 48 S2a = 16
後測 實驗組 n1 = 50 S1b = 8
控制組 n2 = 48 S2b = 14
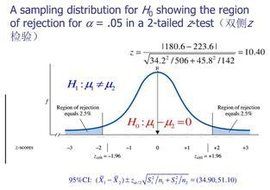
由於n>30,屬於大樣本,所以採用Z檢驗。由於這是檢驗來自兩個不同總體的兩個 樣本平均數,看它們各自代表的總體的差異是否顯著,所以採用雙總體的Z檢驗方法。
計算前要測Z的值:
∵|Z|=0.658<1.96
∴ 前測兩組差異不顯著。
再計算後測Z的值:
∵|Z|= 2.16>1.96
∴ 後測兩組差異顯著。