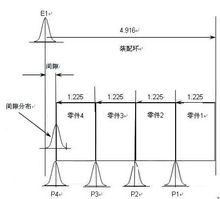
裝配間隙的波動構成統計平方公差法基於這樣一個假設理論：大多數的零部件在它們的公差範圍內呈正態機率分布，此時由它們所構成的系統與各個零部件線性相關，則系統的分布也可以用一個常態分配或近似正態的分布來表示。結合上一個機械系統的案例，這個理論可以用裝配間隙的波動構成圖表示。
統計平方公差法採用統計分析方法進行公差分析，防止了產生過於保守的設計，適當地擴展了零部件的允許公差，如果清楚過程能力，甚至可以得到更寬鬆的公差。
這時候，在同一個機械系統的狀況下，根據統計平方公差法的定義公式，間隙的總公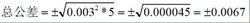差公式：
總共差公式間隙的最小值=0.016-0.0067=0.0093
間隙的最大值=0.016+0.0067=0.0227
也就是說，系統的公差範圍變為[0.0093，0.0227]，相對於極值分析法的結論，它顯得更加接近現實情況。但是，統計平方公差法也存在一個先天性的缺陷：當初始的假定理論不成立，即零部件明顯不呈正態機率分布，或者系統與各個零部件呈非線性相關時，原先統計平方公差的計算公式也就不成立了。
從公式上看，它與RMS（均方根值）相類似，RSS表示一組統計數據的平方和的平方根。
