簡介
在數學中, Lp空間是由p次可積函式組成的空間;對應的 ℓp空間是由 p次可和序列組成的空間。它們有時叫做 勒貝格空間,以昂利·勒貝格命名(Dunford & Schwartz 1958,III.3),儘管依據Bourbaki (1987)它們是Riesz (1910)首先介入。在泛函分析和拓撲向量空間中,他們構成了巴拿赫空間一類重要的例子。 l∞空間是一種所有有界數列構成的空間。
可數維度空間的p-範數
有限維空間中的 p-範數可以如{\displaystyle \mathbb {R} ^{n}}一般定義。當空間維數是可數無限時,也可以將 p-範數的定義拓展到其上。這個定義一般適用於由數列或序列構成的空間,稱為{\displaystyle \ell ^{2}}空間。常見的有如下例子:
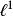 l∞空間
l∞空間空間,所有絕對收斂級數列構成的空間;
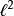 l∞空間
l∞空間空間,所有平方收斂級數列構成的空間;
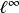 l∞空間
l∞空間空間,所有有界數列構成的空間。
事實上,序列集合上可以自然地按照序列的加法和數乘定義出向量空間。而{\displaystyle \ell ^{p}}空間則是在這個向量空間中定義如下的 p-範數:
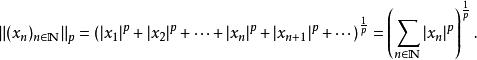 l∞空間
l∞空間然而,上式中右側的級數不總是收斂的(有可能其級數和是無窮大)。所以 l空間實際上是所有序列集合中,令上式右側的級數能夠收斂的元素組成的子集。
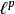 l∞空間
l∞空間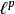 l∞空間
l∞空間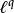 l∞空間
l∞空間可以證明,隨著 p增大, 空間包含的元素也越多。實際上,如果 p< q,那么 空間是 空間的真子集。比如說,以下的數列:
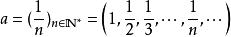 l∞空間
l∞空間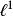 l∞空間
l∞空間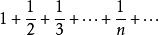 l∞空間
l∞空間不屬 ,因為 的和是無窮大。不過,由於
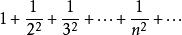 l∞空間
l∞空間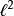 l∞空間
l∞空間Lp空間
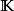 l∞空間
l∞空間當空間維度是無窮而且不可數的時候(沒有一個可數的基底),無法運用有限維或可數維度空間的辦法來定義範數,但對於可積函式空間,仍然能夠定義類似的概念。具體來說,給定可測空間( S, Σ, μ)以及大於等於1的實數 p,考慮所有從 S到域 上的可測函式。考慮所有絕對值的 p次冪在 S可積的函式,也就是集合:
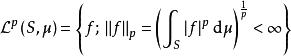 l∞空間
l∞空間集合中的函式可以進行加法和數乘:
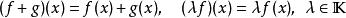 l∞空間
l∞空間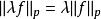 l∞空間
l∞空間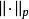 l∞空間
l∞空間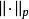 l∞空間
l∞空間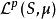 l∞空間
l∞空間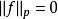 l∞空間
l∞空間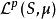 l∞空間
l∞空間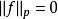 l∞空間
l∞空間從不等式:| f+ g|≤ 2(| f|+ | g|)可知,兩個 p次可積函式的和,也是一個 p次可積函式。另外,容易證明 ;閔可夫斯基不等式的積分形式說明三角不等式對 成立。滿足這樣條件的 構成一個半範數,令 成為一個半賦范向量空間。之所以是半範數,是因為滿足 的函式f不一定是零函式。然而可以通過一套標準的拓撲方法從這個半賦范空間得到一個賦范空間:考慮 中所有使得 的函式f的集合:
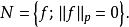 l∞空間
l∞空間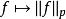 l∞空間
l∞空間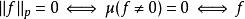 l∞空間
l∞空間集合N可以看作是映射 的零空間。對可測函式f來說, 幾乎處處為零(在測度 μ意義下)。所以
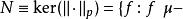 l∞空間
l∞空間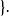 l∞空間
l∞空間幾乎處處為0
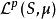 l∞空間
l∞空間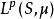 l∞空間
l∞空間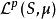 l∞空間
l∞空間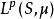 l∞空間
l∞空間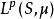 l∞空間
l∞空間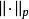 l∞空間
l∞空間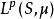 l∞空間
l∞空間而N同時也是 的一個子空間。設 是 關於{\displaystyle N}的商空間。 中的某個元素f可以看作是所有和函式f相差一個N中元素的函式構成的等價類。這樣定義的空間 是一個賦范向量空間,稱為 S上函式關於測度 μ的 L空間。 稱為 函式的 p-範數。
需要注意的是, L空間中的元素嚴格來說並不是具體的函式,而是一族函式構成的等價類。而當需要將 L空間元素當作函式來計算的時候,參與計算的實際是從這一族函式中抽取的一個代表函式。
一致範數與 p-範數之間存在以下關係:
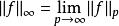 l∞空間
l∞空間可以證明, L空間是完備的空間,也即是說是一個巴拿赫空間(完備賦范向量空間)。 L空間的完備性通常被稱為里茲-費舍爾定理。具體的證明可以藉助測度上的勒貝格積分的相關收斂定理來完成。
參見
•哈代空間
•赫爾德平均
•赫爾德空間
•方均根
