定義
 KMP算法
KMP算法2偽代碼
偽代碼
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | KMP - MATCHER(T,P) n←length[T] m←length[P] π←COMPUTE - PREFIX - FUNCTION(P) q← 0 / / Numberofcharactersmatched. fori← 1ton / / Scanthetextfromlefttoright. dowhileq> 0andP [q + 1 ]≠T[i] doq←π[q] / / Nextcharacterdoesnotmatch. ifP[q + 1 ] = T[i] thenq←q + 1 / / Nextcharactermatches. ifq = m / / IsallofPmatched? thenprint "Patternoccurswithshift" i - m q←π[q] / / Lookforthenextmatch. COMPUTE - PERFIX - FUNCTION(P) m←length[P] π[ 1 ]← 0 k← 0 forq← 2tom dowhilek> 0andP [k + 1 ]≠P[q] dok←π[k] ifP[k + 1 ] = P[q] thenk←k + 1 π[q]←k return π |
Python代碼
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | defprefix( str ): m = len ( str ) pi = [ 0foriinrange (m)] pi[ 0 ] = 0 k = 0 forqinrange( 1 ,m): whilek> 0andstr [k]! = str [q]: k = pi[k - 1 ] ifstr[k] = = str [q]: k = k + 1 pi[q] = k returnpi defmatch(t,p): n = len (t) m = len (p) pi = prefix(p) q = 0 foriinrange( 0 ,n): whileq> 0andp [q]! = t[i]: q = pi[q - 1 ] ifp[q] = = t[i]: q = q + 1 ifq = = m: print ( "matchedin%d.\n" % (i - m + 1 )) print ( "notmatched!\n" ) |
詳細闡述
當我們分析一個模式字元串時,例如:abcabcddes.需要分析一下,每個字元x前面最多有多少個連續的字元和字元串從初始位置開始的字元匹配。然後+1就行了(別忘了,我們的字元串都是從索引1開始的)當然,不要相同位置自己匹配,默認第一個字元的匹配數是0。設字元串為x1,x2,x3...xn,其中x1,x2,x3,...xi,...xn均是字元,設ai為字元xi對應的整數。若且唯若滿足如下條件:字元串x1x2...xmequals字元串x(i-m+1)...xi-1xi並且x1x2...xmx(m+1)unequalsx(i-m)x(i-m+1)...xi-1xi,則a=m。
例如:
abcabcddes
0111234111
|----------------------默認是0
--|||-----------------不能自己在相同位置進行字元匹配,所以這裡認為沒有匹配字元串,所以0+1=1,繼續從1開始匹配
------|||-----------前面的字元和開始位置的字元相同,所以是2,3,4
-----------||||-------不匹配只能取1。
希望能明白的是,如果開始字元是Ch1的話,那么我們就是要在串中第2個Ch1後面的位置開始自己和自己匹配,計算最大的吻合度。
C示例
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 | //c++實現的<a target="_blank" href="/subview/659777/659777.htm">KMP算法</a>,所有涉及字元串,其初始下標從0開始(上述算法均是從1開始) //example:chars[100],t[100];cin>>s>>t;KMP(s,t); //獲取待查詢模式的next數組 int *get_next( char *T, int *next) { inti=0,j=-1; intlength=<a target= "_blank" href= "/subview/736226/5092487.htm" > strlen </a>(T); int *temp=next; *next=-1; <a target= "_blank" href= "/subview/1455003/1455003.htm" > while </a>(i<length) { if (j==-1||*(T+i)==*(T+j)) { i++; j++; //最佳化後的get_next方法,可以防止出現形如"aaaaab"這種模式的計算退化 if (*(T+i)!=*(T+j)) *(next+i)=j; else *(next+i)=*(next+j); } else j=*(next+j); } returntemp; } //<a target="_blank" href="/subview/659777/659777.htm">KMP算法</a> intKMP( char *S, char *T) { intS_Length=<a target= "_blank" href= "/subview/736226/5092487.htm" > strlen </a>(S); intT_Length= strlen (T); //若模式長度大於字元串,則直接返回查詢失敗 if (S_Length<T_Length) return0; inti=0,j=0; int *next=newint[T_Length]; get_next(T,next); <a target= "_blank" href= "/subview/1455003/1455003.htm" > while </a>(i<S_Length&&j<T_Length) { if (j==-1||*(S+i)==*(T+j)) { i++; j++; } else j=*(next+j); } if (j>=T_Length) returni-T_Length; return0; } |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 | #include<iostream> #include<string.h> intnext[100]; voidgetnext(charb[]) { inti=1,j=0; //i是每個位子,j是回退的位子 next[1]=0; <a target= "_blank" href= "/subview/1455003/1455003.htm" > while </a>(i<=<a target= "_blank" href= "/subview/736226/5092487.htm" > strlen </a>(b)) { if (j==0||b[i-1]==b[j-1]) { i++; j++; next[i]=j; } else j=next[j]; //用上一個的回退關係 } } intkmp(chara[],charb[]) { inti=1,j=1; //i是<a target="_blank" href="/subview/5594190/5635509.htm">主串</a>中的位子,j匹配串的位子 <a target= "_blank" href= "/subview/1455003/1455003.htm" > while </a>(i<=<a target= "_blank" href= "/subview/736226/5092487.htm" > strlen </a>(a)&&j<= strlen (b)) { if (j==0||a[i-1]==b[j-1]) { i++; j++; } else j=next[j]; } if (j> strlen (b)) returni- strlen (b); else return0; } intmain() { chara[40],b[40]; <a target= "_blank" href= "/subview/410546/410546.htm" > printf </a>( "要匹配的<a target=" _blank " href=" /subview/5594190/5635509.htm ">主串</a>:\n" ); <a target= "_blank" href= "/subview/1390039/1390039.htm" > scanf </a>( "%s" ,a); printf ( "要匹配的目標字元串:\n" ); scanf ( "%s" ,b); getnext(b); printf ( "輸出next值:\n" ); for (inti=1;i<=<a target= "_blank" href= "/subview/736226/5092487.htm" > strlen </a>(b);i++) printf ( "%d" ,next[i]); <a target= "_blank" href= "/subview/410546/410546.htm" > printf </a>( "\n" ); printf ( "%d" ,kmp(a,b)); <a target= "_blank" href= "/subview/627587/14965930.htm" > system </a>( "pause" ); main(); return0; } |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | voidGetNext( char *T, int *next) { intk=1,j=0; next[1]=0; while (k<T[0]) { if (j==0||T[k]==T[j]) { ++k; ++j; next[k]=j; } else j=next[j]; } } |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | voidGetNextEx( char *T, int *next) { intk=1,j=0; next[1]=0; <a target= "_blank" href= "/subview/1455003/1455003.htm" > while </a>(k<<a target= "_blank" href= "/subview/736226/5092487.htm" > strlen </a>(T)) { if (j==0||T[k]==T[j]) { ++k; ++j; if (T[k]==T[j]) next[k]=next[j]; else next[k]=j; } else j=next[j]; } } |
相當簡單:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | intKMP( char *S, char *T,intpos) { intk=pos,j=1; inttt=<a target= "_blank" href= "/subview/736226/5092487.htm" > strlen </a>(S); <a target= "_blank" href= "/subview/1455003/1455003.htm" > while </a>(k<tt) { if (S[k]==T[j]) { ++k; ++j; } else j=next[j]; } if (j>T[0]) returnk-T[0]; else return0; } |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | //findatemplateinastring. #include<string.h> #include<stdio.h> intIndex( char *S, char *T,intpos) //pos記錄從哪一位開始匹配可以直接用0代替 { intk=pos,j=0; <a target= "_blank" href= "/subview/1455003/1455003.htm" > while </a>(k<<a target= "_blank" href= "/subview/736226/5092487.htm" > strlen </a>(S)&&j< strlen (T)) //未超出字元串的長度 { if (S[k+j]==T[j]) ++j; //如果相同,則繼續向後比較 else { k++; j=0; } //如果不同,就回溯,重新查找 } if (j== strlen (T)) returnk; else return0; } |
實際套用
用KMP算法,計算串的最大匹配論文摘要
給定兩個串S和T,長分別m和n,本文給出了一個找出二串間最大匹配的算法。該算法可用於比較兩個串S和T的相似程度,它與串的模式匹配有別。
關鍵字
模式匹配串的最大匹配算法
AlgorithmonMaximalMatchingofStrings
LinYuCaiXiangYongHongZhangChunXiaZhangJianJun
(ComputerScienceDepartmentofYunnanNormalUniversityKunming650092)
ABSTRACTGivenTwoStringsSoflengthmandToflengthn,thepaperpresentsanalgorithmwhichfindsthemaximalmatchingofthem.ThealgorithmcanbeusedtocomparethesimilarilityofthetwostringsSandT,itisdifferentwiththestrings'pattrenmatching.
KEYWORDSPatternMatchingMaximalMatchingofStringsAlgorithm
提出問題
字元串的模式匹配主要用於文本處理,例如文本編輯。文本數據的存儲(文本壓縮)和數據檢索系統。所謂字元串的模式匹配[2],就是給定兩個字元串S和T,長度分別為m和n,找出T中出現的一個或多個或所有的S,在這方面已經取得了不少進展。本文從文本處理的另一個角度出發,找出兩個串的最大匹配,比較其相似程度。它主要套用於文本比較,特別是在計算機輔助教學中。顯然前者要找S的完全匹配,而後者並無此要求。例如,若S=ABCD,T=EFABCDX,那么模式匹配的結果就是找出了T中的一個ABCD,而我們算法的結果就是S能與T的ABCD完全匹配,但是T中還有3個字元是比S多出來的,也就是說在S中有100%的字元與T中的匹配,而在T中有57%的字元與S中的匹配。若S=ABCDFE,T=AFXBECDY。則在模式匹配中S與T無匹配項,但在我們的算法中就能發現T中存在A,B,C,D,但D後不存在E,F。而且S中也存在A,B,C,D,且具有順序性。這樣就能公正地評價S,T的區別。得知其相似程度。
文章的組織如下:首先介紹基本定義和問題的描述;第三節是算法設計;最後是本文總結。
問題描述
設∑為任意有限集,其元稱為字元,w:∑→N為∑到N的函式,稱為∑的權函式(註:本文僅討論權值恆為1的情況)。∑*為∑上的有限字元串集合,那么對任意S,T∈∑*,設S=a1a2…am,T=b1b2…bn,m>0,n>0。記<m>={1,2,…,m},<n>={1,2,…,n},則稱{(i,j)∣i∈<m>;,j∈<n>;,ai=bj}為S與T的匹配關係集,記作M(S,T),稱M為S與T的一個(容許)匹配,若對任意(i,j),(i',j')∈,①i<i',若且唯若j<j',②i=i'若且唯若j=j'。S與T的匹配中滿足最大者,稱為S與T的最大匹配。若C(i,j)為N上的m×n矩陣,且滿足:
則稱矩陣C為串S與T的匹配關係陣。
於是求串S與T的最大匹配,等價於求C中的一個最大獨立點集M,它滿足,若ci,j,ci',j'∈M,則i<i'若且唯若j<j',i=i'若且唯若j=j'。我們稱這樣的最大獨立點集為C的最大C-獨立點集。
例:設∑為所有字母的集合,對任意x∈∑,w(x)≡1,設S與T分別為:S=“BOOKNEWS”,T=“NEWBOOKS”。則我們可以得到S與T兩個匹配:
這裡=5;
這裡=4。
顯然為串S與T的最大匹配。
S與T的匹配關係陣C可表示如下:
其中帶圈的部分為一最大C-獨立點集。
設計
我們僅就權值為一的情況進行討論。
設S和T為任意給定串,C為的S與T匹配關係陣,那么由2的討論知,求S與T的最大匹配問題,等價於求C的最大C-獨立點集問題。因而,為了解決我們的問題,只要給出求C的最大C-獨立點集的算法就可以了。
顯然,為了求出C的最大C-獨立點集,我們可以採用這樣的方法:搜尋C的所有C-獨立點集,並找出它的最大者。這種方法是可行的,但並不是非常有效的。這會使問題變得很繁,複雜度很大。因此,我們先對問題進行分析。
在下面的討論中,我們把C的任一C-獨立點集={ai1,j1,…,ais,js},記作=ai1,j1…ais,js,i1<;…<is。於是可看作陣C中以1為節點的一條路,滿足:對路中的任意兩節點,均有某一節點位於另一節點的右下方。稱這種路為右下行路。
於是求C-獨立點集等價於求陣C的右下行路。這種求右下行路的搜尋可以逐行往下進行。
命題1.若=αai,jβ和ψ=α'ai,jσ為C的兩個C-獨立點集,且α為α'的加細,則存在C-獨立點集'=αai,jδ,滿足≥。
命題2.若=αai,jβ和ψ=α'ai+k,jσ為C的兩個C-獨立點集,且≥,則存在C-獨立點集'=αai,jδ,滿足≥。
命題3.若=αai,jβ和ψ=α'ai,j+kσ為C的兩個C-獨立點集,且≥,則存在C-獨立點集'=αai,jδ,滿足≥。
由命題1知,在搜尋右下行路的過程中,如果已獲得了某一C-獨立點集的某一初始截段αai,j和另一C-獨立點集ψ的某一初始截段α'ai,j,且有≤,則我們可以停止對ψ的進一步搜尋。
由命題2知,在搜尋右下行路的過程中,在某一列j存在某兩個C-獨立點集的某初始截段=ai1,j1…ais,j和ψ=al1,m1…alt,j,如果≥,但lt>is,則我們可以停止對ψ的進一步搜尋。
由命題3知,在搜尋右下行路的過程中,在某一行i存在某兩個C-獨立點集的某初始截段=ai1,j1…ai,js和ψ=ai1,m1…ai,mt,如果≥,但mt>js,則我們可以停止對ψ的進一步搜尋。
由此可見,並不要求搜尋所有C的最大C-獨立點集,而可以採用比這簡單得多的方法進行計算。那么按照我們上面的三個命題,來看如下實例:
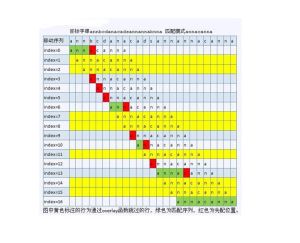
首先我們得到=B(在上的節點用①表示),我們向右下方找路,可以發現,在第4列有兩個1,根據命題2,我們選擇上面的一個1,也就是說選擇第1行的那個1,而不要第2行的那個1。同時我們也發現在第1行也有兩個1,由命題3知,我們選擇左邊的那個1,即第4列的那個1。此時=BO。但是當我們的算法運行到第4行時,=BOOK,由於K在第3行第6列,而本行的1在第1列,在路最後一個節點K的左邊,那么我們必須新建一條路ψ,因為我們並不能確定是否以後就有≥,當算法運行到第6行時,=BOOK,ψ=NEW,=4,=3,我們將S鏈到路上,此時我們得到最長右下行路=BOOKS,=5。這樣我們就可以計算出這兩個字元串的匹配程度。
在我們的算法設計過程中,用到了兩個技巧。技巧之一,矩陣C不用存儲,是動態建立的,節省了空間。技巧之二,本算法並不要求所有的S與T中所有的元素都相互進行比較,也並不存儲所有的右下行路,節省了時間和空間。由矩陣中1的出現情況可見,本算法所需的空間和時間都遠小於O(mn)
結束語
本文給出了一個與模式匹配不同的,具有若干套用的,串的最大匹配算法,該算法已經在機器上實現,達到了預期的效果。本文僅討論權值恆為1的情況,對於權值任意的情形不難由此得到推廣。