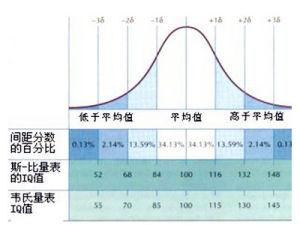
特點
標準分數可以回答這樣一個問題:"一個給定分數距離平均數多少個標準差?"在平均數之上的分數會得到一個正的標準分數,在平均數之下的分數會得到一個負的標準分數。
標準分數是一種可以看出某分數在分布中相對位置的方法。標準分數能夠真實的反應一個分數距離平均數的相對標準距離。如果我們把每一個分數都轉換成標準分數,那么每一個標準分數會以標準差為單位表示一個具體分數到平均數的距離或離差。
將成常態分配的數據中的原始分數轉換為標準分數,我們就可以通過查閱標準分數在正態曲線下面積的表格來得知平均數與標準分數之間的面積,進而得知原始分數在數據集合中的百分等級。
一個數列的各標準分數的平方和等於該數列數據的個數,並且標準分數的標準差和方差都為1。.
套用
在日本,標準分數常被用在計算學力測驗的"學力偏差值",並且依此判斷進入理想大學的可能性。在智力測驗時,用來計算"智力標準分數",在教育的用途上,常和"智商"一起被當作參考的依據。
在智力測驗時,用來計算"智力標準分數",在教育的用途上,常和"智商"一起被當作參考的依據。 自1988年起,中國廣東的聯考實施標準分制度。但標準分有一致命弱點,若成績有誤,分數將難以修改,可以引發數千乃至上萬人的分數需要修正,因為它是以名次或順序來計分。
類似個案,像詞作家陳小奇懷疑分數有誤,一查分數相差幾十分,修正後才得以進入中山大學,不然,也只能上箇中專,但很多人可能沒他那么好運,因此標準分很可能會埋沒一些潛在人才。有鑒於此,到2006年止,標準分正式壽終正寢,原始分制度再次啟用。
標準化
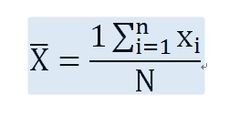 標準分數
標準分數 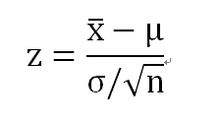 標準分數
標準分數 在數理統計學中,隨機變數“X”是使用理論(母體)的平均值和標準差所標準化的結果:
Z=(x-μ)/σ
其中 μ = E(X) 為平均值
σ² = Var(X)X的機率分布之方差
若隨機變數無法確定時
則為算術平均數:
因此經過標準化的結果為:
例如:
某中學高(1)班期末考試,已知語文期末考試的全班平均分為73分,標準差為7分,甲得了78分;數學期末考試的全班平均分為80分,標準差為6.5分,甲得了83分。甲哪一門考試成績比較好?
因為兩科期末考試的標準差不同,因此不能用原始分數直接比較。需要將原始分數轉換成標準分數,然後進行比較。
Z(語文)=(78-73)/7=0.71 Z(數學)=(83-80)/6.5=0.46
甲的語文成績在其整體分布中位於平均分之上0.71個標準差的地位,他的數學成績在其整體分布中位於平均分之上0.46個標準差的地位。
由此可見,甲的語文期末考試成績優於數學期末考試成績。
由於標準分數不僅能表明原始分數在分布中的地位,它還是以標準差為單位的等距量表,故經過把原始分數轉化為標準分數,可以在不同分布的各原始分數之間進行比較。