基本介紹
定義1Skolem標準型是如下任意一種形式的一階命題:
(∏∑型)
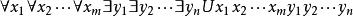 Skolem標準型
Skolem標準型(1)
(∏或∑型 )
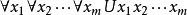 Skolem標準型
Skolem標準型(2)(∏型)
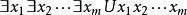 Skolem標準型
Skolem標準型(3)(∑型)
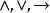 Skolem標準型
Skolem標準型其中,U是不包含量詞且連線符僅僅為的公式。
 Skolem標準型
Skolem標準型 Skolem標準型
Skolem標準型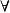 Skolem標準型
Skolem標準型 Skolem標準型
Skolem標準型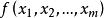 Skolem標準型
Skolem標準型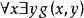 Skolem標準型
Skolem標準型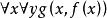 Skolem標準型
Skolem標準型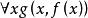 Skolem標準型
Skolem標準型 Skolem標準型
Skolem標準型 Skolem標準型
Skolem標準型 Skolem標準型
Skolem標準型 Skolem標準型
Skolem標準型 Skolem標準型
Skolem標準型 Skolem標準型
Skolem標準型第(1)種標準型顯然借鑑了亞里士多德三段論的直言命題的形式。第(1)、(3) 種標準型中的是可以消除的。消除的方法有三種。第一種是將公式中的換為,然後對於原來的約束項變為它前面的變數確定的新的變數,這樣原來的公式成為僅由全稱量詞約束的公式,原來的存在量詞約束的項的解釋縮小為由它前面的項所確定的量。如轉換為,也可寫成。如果有明確的y的解釋域,這種轉換後新的公式沒有改變與原有公式的真假值的等價性;否則真假值的等價性可能有變。第二種是將(1)公式中的換為,然後對於對U增加解釋性的關係,使得公式對於原來公式的域中不能滿足的的項增補一個非關係,進而擴大了y 的解釋域。第三種是將公式中的去掉,然後對於原來的約束項變為一個確定的解釋域中的項a,原有公式的真假值的等價性遭到破壞,但是在確定公式的無效性(永假) 時,改變後的公式與原公式具有同等意義。無論哪種方法都可以消除存在量詞。用上述同樣的方法,顯然,也可以將一階公式轉換為標準型(注意轉變後其有效性可能與原公式並不完全等價)。
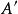 Skolem標準型
Skolem標準型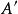 Skolem標準型
Skolem標準型總之,對於一階命題(公式)的Skolem 標準化,是基於 Skolem 標準化的定理:對於任何一階命題A,都存在一個標準型命題,使得當是可滿足的,A在其解釋域是可滿足的。
定理1 一階公式G 與G的子句集S並不相等,但是它們具有相同的不可滿足性。
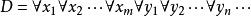 Skolem標準型
Skolem標準型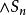 Skolem標準型
Skolem標準型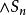 Skolem標準型
Skolem標準型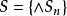 Skolem標準型
Skolem標準型證明:如果公式G 是∏型,解釋G 的域,這與子句集解釋S的域完全重合。同時,G 不能滿足,也就意味著中至少有一個子句不能滿足,此時為0;由於,此時S也為0,即Ⅱ型的不可滿足性與子句集S的不可滿足性完全相同。
 Skolem標準型
Skolem標準型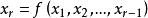 Skolem標準型
Skolem標準型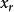 Skolem標準型
Skolem標準型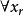 Skolem標準型
Skolem標準型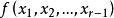 Skolem標準型
Skolem標準型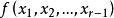 Skolem標準型
Skolem標準型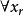 Skolem標準型
Skolem標準型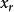 Skolem標準型
Skolem標準型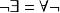 Skolem標準型
Skolem標準型 Skolem標準型
Skolem標準型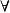 Skolem標準型
Skolem標準型 Skolem標準型
Skolem標準型 Skolem標準型
Skolem標準型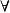 Skolem標準型
Skolem標準型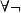 Skolem標準型
Skolem標準型如果公式G 是∏∑型或∑型,此時G將有約束的項,如果子句集中對於的解釋域設定為將與的解釋域可能不一致。但是,對於不可滿足性而言,“沒有任何一個解釋滿足G 中構成的公式”和“均不可滿足S中構成的公式”在邏輯上是一致的。可參照直言命題量詞的否定運算規則,即,它是說,“不存在”(即的不可滿足性) 意味著“”所描述的(與約束的項的)域“全都不”滿足。“”是表述在G中:而“”表述在子句集中——因為子句不再表示量詞約束意味著以項的全稱為解釋域,恰好表達了所有解釋的不滿足性。
 Skolem標準型
Skolem標準型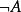 Skolem標準型
Skolem標準型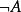 Skolem標準型
Skolem標準型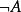 Skolem標準型
Skolem標準型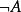 Skolem標準型
Skolem標準型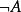 Skolem標準型
Skolem標準型定理1的啟示在於,對於∏∑型或∑型的一階公式,如果證明其不可滿足性,可以證明其替換之後形成的Ⅱ型公式。這是歸結證明的一個重要思想,即要證明命題A,只要證明不可滿足(反證法的運用);要證明的不可滿足,只要證明的子句集的不可滿足;而要證明的子句集的不可滿足,只要證明的Herbrand域的不可滿足 。
Skolem標準範式
定義2以前束範式中消去全部存在量詞所得到的公式即為 斯柯林(Skolem)標準範式。
 Skolem標準型
Skolem標準型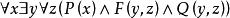 Skolem標準型
Skolem標準型例如,如果用Skolem函式代替前束範式中的y即得到Skolem標準範式:
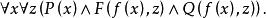 Skolem標準型
Skolem標準型Skolem標準型的一般形式是
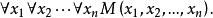 Skolem標準型
Skolem標準型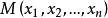 Skolem標準型
Skolem標準型其中,是一個合取範式,稱為 Skolem標準型的母式。
將謂詞公式G化為Skolem標準型的步驟如下:
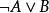 Skolem標準型
Skolem標準型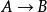 Skolem標準型
Skolem標準型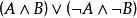 Skolem標準型
Skolem標準型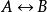 Skolem標準型
Skolem標準型(1) 消去謂詞公式G中的蘊涵(→) 和雙條件符號(↔),以代替以代替。
 Skolem標準型
Skolem標準型 Skolem標準型
Skolem標準型(2) 減小否定符號() 的轄域,使否定符號“”最多只作用到一個謂詞上。
(3) 重新命名變元名,使所有的變元的名字均不同,並且自由變元及約束變元亦不同。
(4) 消去存在量詞。這裡分兩種情況,一種情況是存在量詞不出現在全稱量詞的轄域內,此時,只要用一個新的個體常量替換該存在量詞約束的變元,就可以消去存在量詞;另一種情況是存在量詞位於一個或多個全稱量詞的轄域內,這時需要用一個Skolem函式替換存在量詞而將其消去。
(5) 把全稱量詞全部移到公式的左邊,並使每個量詞的轄域包括這個量詞後面公式的整個部分。
(6) 母式化為合取範式:任何母式都可以寫成由一些謂詞公式和謂詞公式否定的析取的有限集組成的合取。
需要指出的是,由於在化解過程中,消去存在量詞時作了一些替換,一般情況下,公式G的Skolem標準型與G 並不等值 。
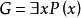 Skolem標準型
Skolem標準型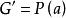 Skolem標準型
Skolem標準型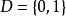 Skolem標準型
Skolem標準型 Skolem標準型
Skolem標準型例1,消去存在量詞後得,若論域是,取D下的一個解釋:
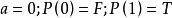 Skolem標準型
Skolem標準型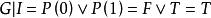 Skolem標準型
Skolem標準型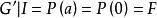 Skolem標準型
Skolem標準型 Skolem標準型
Skolem標準型,顯然G與不等價 。
Skolem函式
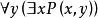 Skolem標準型
Skolem標準型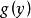 Skolem標準型
Skolem標準型定義3如果存在量詞在全稱量詞的轄域內,如公式,變數x的取值依賴於變數y的取值,令這種依賴關係由函式來表示,它把每個y值映像到存在的那個x,這個函式稱為 斯柯林(Skolem)函式 。
 Skolem標準型
Skolem標準型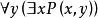 Skolem標準型
Skolem標準型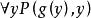 Skolem標準型
Skolem標準型如果用Skolem函式代替存在的個體,就可以消去存在量詞。注意,這裡的函式應是原合式公式中沒有的符號。公式可化為。

