概念
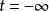 S矩陣
S矩陣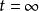 S矩陣
S矩陣考察微觀粒子所組成的系統散射或反應過程時,需要研究的是在一定的相互作用下,系統從一定的初始狀態如何隨時間演化。絕熱近似下,微觀粒子系統從時間的初始狀態躍遷到時間的末態過程的機率振幅就是S矩陣的一個矩陣元,它的絕對值二次方就是該躍遷過程的機率。所以當某S矩陣元為零時,該躍遷過程就是禁戒的。所有可能的S矩陣元的整體構成S矩陣。
基本原理
S矩陣與微觀粒子間的相互作用有關,但S矩陣的某些普遍性質則並不依賴於相互作用的具體機制。從任一特定初態出發,到一切可能末態機率之和必須等於1,這在數學上反映為S矩陣是么正矩陣,即具有么正性。
 S矩陣
S矩陣一切物理過程必須符合相對論的因果性條件,這在數學上反映為S矩陣元的解析性。一切物理過程都保持能量守恆和動量守恆,這在數學上反映為S矩陣元中包含有體現這些守恆定律的函式因子。此外,角動量守恆定律、電荷守恆定律以及各種不同相互作用分別具有的特殊的對稱性和守恆律,都會對S矩陣元給出一定的限制。這些限制中最常見的是給出某些S矩陣元之間滿足一定的等式或給出某些S矩陣元必須等於零,後者即通常所說的選擇定則。
即使已知微觀粒子之間相互作用的基本規律,要從理論上計算S矩陣仍是困難的。相互作用很弱的情形下,可用微擾論的方法在足夠好的近似下求出S矩陣元。但在相互作用較強時,微擾論的方法就不再適用。
20世紀50年代到60年代,從S矩陣的么正性、解析性以及滿足的一些基本的對稱性要求出發,建立和發展了色散關係的理論,得到了一些不依賴於微擾論的普遍結果,並為以後用非微擾方法研究S矩陣的性質打下了基礎。

