PolyLog —普通和尼爾森(Nielsen)廣義的對數函式
……
Li_-1(x)=∫(Li_-2(x))/x dx=∫(1-x)^(-2)+(2x)/(1-x)^3 dx=x/(1-x)^2
Li_0(x)=∫(Li_-1(x))/x dx=∫x/(1-x)^2 dx =x/(1-x)
Li_1(x)=∫(Li_0(x))/x dx=∫1/(1-x) dx=-ln(1-x)
Li_2(x)=∫(Li_1(x))/x dx=∫-(ln(1-x))/x dx
Li_3(x)=∫(Li_2(x))/x dx
……(_表示下標)
對於Li_n(x) (n∈Z)有關係式:
Li_(n+1)(x)=∫(Li_n(x))/x dx
推廣到n∈R,甚至n∈C,該關係式都成立,
另外,當|x|<1 時,有關係式:(n∈C)
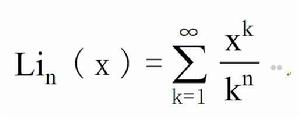 Li_n(x)
Li_n(x)x∈C時,Li_n(x)表達式為:
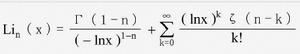 Li_n(x) x∈C
Li_n(x) x∈C其中Γ(x)=(x-1)!是Gamma函式,ζ(x)是Riemann 函式(zeta函式)
PolyLog 函式通常用於對數積分,是數學中的特殊函式。