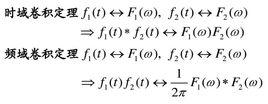定理
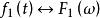 卷積定理
卷積定理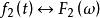 卷積定理
卷積定理 卷積定理
卷積定理若 , , 表示傅立葉變換。則
時域卷積定理
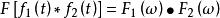 卷積定理
卷積定理 卷積定理
卷積定理表示卷積。時域卷積定理表明兩信號在時域的卷積積分對應於在頻域中該兩信號的傅立葉變換的乘積。
頻域卷積定理
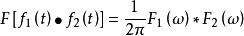 卷積定理
卷積定理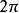 卷積定理
卷積定理頻域卷積定理表明兩信號在時域的乘積對應於這兩個信號傅立葉變換的卷積除以 。
卷積定理揭示了時間域與頻率域的對應關係。
這一定理對Laplace變換、Z變換、Mellin變換等各種傅立葉變換的變體同樣成立。需要注意的是,以上寫法只對特定形式的變換正確,因為變換可能由其它方式正規化,從而使得上面的關係式中出現其它的常數因子。
推導過程
證明卷積定理前,先對證明中用到的性質進行簡單介紹。
 卷積定理
卷積定理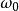 卷積定理
卷積定理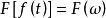 卷積定理
卷積定理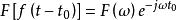 卷積定理
卷積定理傅立葉變換的時移性質。該性質表述為:設 、 為實常數,若 ,則 。
傅立葉變換的時移性質表明當一個信號沿時間軸平移後,各頻率成份的大小不發生改變,但相位發生變化。該性質可以由傅立葉變換的定義進行證明:
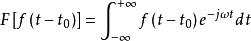 卷積定理
卷積定理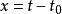 卷積定理
卷積定理令 ,則有
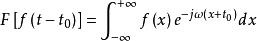 卷積定理
卷積定理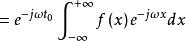 卷積定理
卷積定理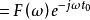 卷積定理
卷積定理另外,由富比尼定理可知,積分區域連續的前提下,二重積分的積分次序可以交換。
下面對時域卷積定理和頻域卷積定理進行推導證明。
時域定理證明
首先,卷積定義為
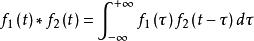 卷積定理
卷積定理然後,代入傅立葉變換公式
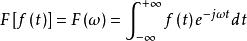 卷積定理
卷積定理由此可得
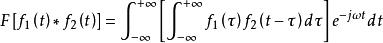 卷積定理
卷積定理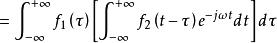 卷積定理
卷積定理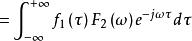 卷積定理
卷積定理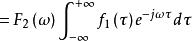 卷積定理
卷積定理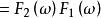 卷積定理
卷積定理至此,時域卷積定理得證 。
頻域定理證明
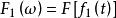 卷積定理
卷積定理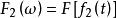 卷積定理
卷積定理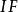 卷積定理
卷積定理設 , , 表示傅立葉逆變換,則
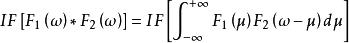 卷積定理
卷積定理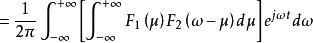 卷積定理
卷積定理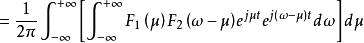 卷積定理
卷積定理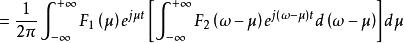 卷積定理
卷積定理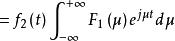 卷積定理
卷積定理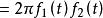 卷積定理
卷積定理因此有
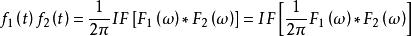 卷積定理
卷積定理故頻域卷積定理得證。
套用
卷積定理的套用在很多涉及積分變換、積分方程的文章中都有所體現。常見的一些重要的積分變換,例如:Mellin變換、Laplace變換、Fourier變換等都具有所謂的卷積性質(Convolution Property)。這裡要注意的是,針對不同的積分變換,卷積性質的形式不是完全相同的,只要一些基本的結構得到保留就可以了。
Fourier變換
1、時域卷積定理與傅立葉變換性質的關係
(1) 時移性質
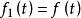 卷積定理
卷積定理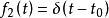 卷積定理
卷積定理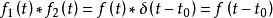 卷積定理
卷積定理在時域中,設 , ,由於 ,即時移。
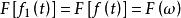 卷積定理
卷積定理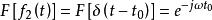 卷積定理
卷積定理在頻域中,設 ,由於 ,根據時域卷積定理有:
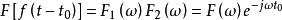 卷積定理
卷積定理該公式表示的就是傅立葉變換的時移性質。
(2) 時域微分性質
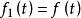 卷積定理
卷積定理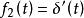 卷積定理
卷積定理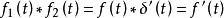 卷積定理
卷積定理在時域中,設 , ,由於 ,即時域微分。
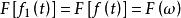 卷積定理
卷積定理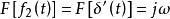 卷積定理
卷積定理在頻域中,設 ,由於 ,根據時域卷積定理有:
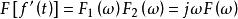 卷積定理
卷積定理該公式表示的就是傅立葉變換的時域微分性質。
(3) 時域積分性質
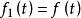 卷積定理
卷積定理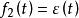 卷積定理
卷積定理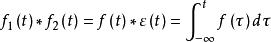 卷積定理
卷積定理在時域中,設 , ,由於 ,即時域積分。
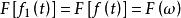 卷積定理
卷積定理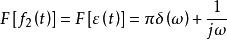 卷積定理
卷積定理在頻域中,設 ,由於 ,根據時域卷積定理有:
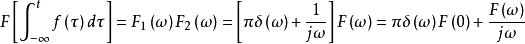 卷積定理
卷積定理該公式表示的就是傅立葉變換的時域積分性質。
(4) 系統函式
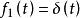 卷積定理
卷積定理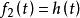 卷積定理
卷積定理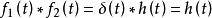 卷積定理
卷積定理在時域中,設 , ,由於 ,即系統衝激回響。
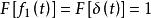 卷積定理
卷積定理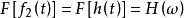 卷積定理
卷積定理在頻域中,由於 , ,根據時域卷積定理有:
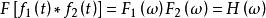 卷積定理
卷積定理該公式表示的就是系統函式 。
(5) 系統的零回響狀態
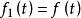 卷積定理
卷積定理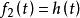 卷積定理
卷積定理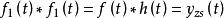 卷積定理
卷積定理在時域中,設 , ,由於 ,即系統的零回響狀態。
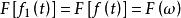 卷積定理
卷積定理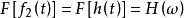 卷積定理
卷積定理在頻域中,設 , ,根據時域卷積定理有:
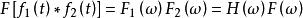 卷積定理
卷積定理該公式表示的就是零狀態回響的頻域分析法 。
(6) 系統的無失真傳輸條件
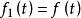 卷積定理
卷積定理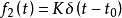 卷積定理
卷積定理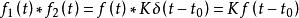 卷積定理
卷積定理在時域中,設 , ,由於 ,即系統無失真傳輸。
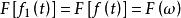 卷積定理
卷積定理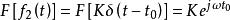 卷積定理
卷積定理在頻域中,設 ,由於 ,根據時域卷積定理有:
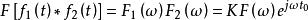 卷積定理
卷積定理該公式表示的就是系統的無失真傳輸條件。
(7) 正弦穩態回響
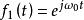 卷積定理
卷積定理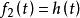 卷積定理
卷積定理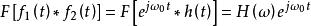 卷積定理
卷積定理在時域中,設 , ,由於 ,即系統正弦穩態回響。
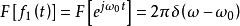 卷積定理
卷積定理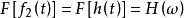 卷積定理
卷積定理在頻域中,設 , ,根據時域卷積定理有:
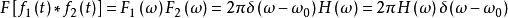 卷積定理
卷積定理該公式表示的就是系統正弦穩態回響的頻域分析法。
2、頻域卷積定理與傅立葉變換性質的關係
(1) 頻移性質
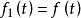 卷積定理
卷積定理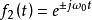 卷積定理
卷積定理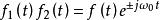 卷積定理
卷積定理在時域中,設 , ,則 。
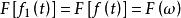 卷積定理
卷積定理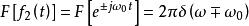 卷積定理
卷積定理在頻域中,設 ,由於 ,根據頻域卷積定理有:
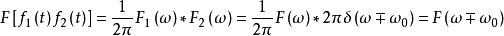 卷積定理
卷積定理該公式表示的就是傅立葉變換的頻移性質。
(2) 頻域微分性質
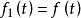 卷積定理
卷積定理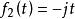 卷積定理
卷積定理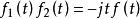 卷積定理
卷積定理在時域中,設 , ,則 。
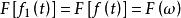 卷積定理
卷積定理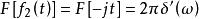 卷積定理
卷積定理在頻域中,設 ,由於 ,根據頻域卷積定理有:
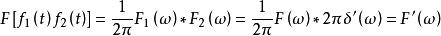 卷積定理
卷積定理該公式表示的就是傅立葉變換的頻域微分性質。
(3) 調製
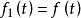 卷積定理
卷積定理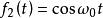 卷積定理
卷積定理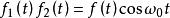 卷積定理
卷積定理在時域中,設 , ,則 ,即振幅調製。
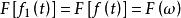 卷積定理
卷積定理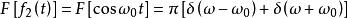 卷積定理
卷積定理在頻域中,設 ,由於 ,根據頻域卷積定理有:
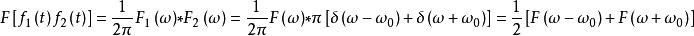 卷積定理
卷積定理該公式表示的就是振幅調製定理 。
其他套用
 卷積定理
卷積定理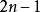 卷積定理
卷積定理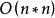 卷積定理
卷積定理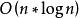 卷積定理
卷積定理卷積定理還可以簡化卷積的運算量。對於長度為 的序列,按照卷積的定義進行計算,需要做 組對位乘法,其計算複雜度為 ;而利用傅立葉變換將序列變換到頻域上後,只需要一組對位乘法,利用傅立葉變換的快速算法之後,總的計算複雜度為 。這一結果可以在快速乘法計算中得到套用。