內容
Lotka-Volterra模型(Lotka-Volterra種間競爭模型)是logistic模型(阻滯增長模型)的延伸。現設定如下參數:
N1、N2:分別為兩個物種的種群數量
K1、K2:分別為兩個物種的環境容納量
r1、r2 :分別為兩個物種的種群增長率
依邏輯斯蒂模型有如下關係:
dN1 / dt = r1 N1(1 - N1 / K1)
其中:N/K可以理解為已經利用的空間(稱為“已利用空間項”),則(1-N/K)可以理解為尚未利用的空間(稱為“未利用空間項”)
當兩個物種競爭或者利用同一空間時,“已利用空間項”還應該加上N2種群對空間的占用。則:
dN1 / dt = r1 N1(1 - N1 / K1 - αN2 / K1) ————(1)
其中,α:物種2對物種1的競爭係數,即每個N2個體所占用的空間相當於α個N1個體所占用空間。
則有,β:物種1對物種2的競爭係數,即每個N1個體所占用的空間相當於β個N2個體所占用空間。則另有:
dN2 / dt = r2 N2(1 - N2 / K2 - βN1 / K2) ————(2)
如我們所知:
當物種N1種群(物種1)的環境容納量為K1時,N1種群中每個個體對自身種群的增長抑制作用為1/K1;
同理,N2種群中每個個體對自身種群的增長抑制作用為1/K2。
另外,從(1)、(2)兩個方程以及α、β的定義中可知:
N2種群中每個個體對N1種群的影響為:α/K1
N1種群中每個個體對N2種群的影響為:β/K2
因此,當物種2可以抑制物種1時,可以認為,物種2對物種1的影響 > 物種2對自身的影響,即 α/K1 > 1/K2。
整理後得:K2 > K1/α,同理有:
物種2不能抑制物種1:K2 < K1/α
物種1可以抑制物種2:K1 > K2/β
物種1不能抑制物種2:K1 < K2/β
這樣,在競爭的過程中,由於K1、K2、α 以及 β 的數值不同,可能會產生如下四種結果:
| 物種1能抑制物種2 (K1 > K2/β) | 物種1不能抑制物種2 (K1 < K2/β) | |
| 物種2能抑制物種1 (K2 > K1/α) | 兩物種都有可能得勝 (結果3) | 物種2總是得勝 (結果2) |
| 物種2不能抑制物種1 (K2 < K1/α) | 物種1總是得勝 (結果1) | 兩物種都不能抑制對方 (結果4:穩定平衡) |
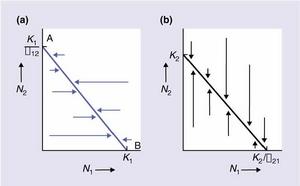
那么,當N2種群達到何種密度時,剛好使N1種群保持在0水平上?換言之,每個種群達到什麼樣的密度時才能阻止另一個種群的增長呢?
結論是,N2種群達到K1/α,N1就再也不能增長
或者說,N1種群達到K2/β,N2就再也不能增長
可以得到兩個物種的各自的平衡線如下:
將兩平衡線疊合起來,則得到四種不同的結局:
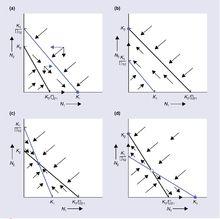 Lotka-Volterra模型
Lotka-Volterra模型何為平衡呢,就是N1和N2種群的數量都不發生變化,即:
N1 / dt = r1 N1(1 - N1 / K1 - αN2 / K1)= 0.........(1)
N2 / dt = r2 N2(1 - N2 / K2 - βN1 / K2)= 0.........(2)
滿足兩個方程時,兩種種群平衡,則顯然交點即是平衡點。
那么,對於結果1和結果2,兩個種群的平衡線沒有交點,則不可能達到平衡,總是有一方最終被完全排擠掉。
結果3雖然存在一個平衡點,但是很不穩定,只要自然條件的微小波動造成偏離平衡點,那么其中占優的一方就會最終取得生存競爭的勝利。
結果4是一個穩定的平衡,無論N1和N2種群數量的組合(N1,N2)落在直角坐標系內哪一區域,最終都將使得N1種群和N2種群的數量趨向平衡點。
註:該模型建立的基礎是種群1個體與種群2個體所占空間的大小(體型,更進一步就是掠食範圍,領地等)來衡量兩者之間的競爭大小。