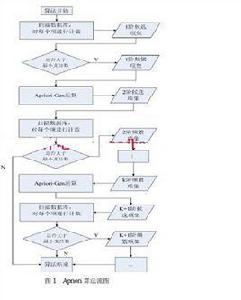
算法背景
提出背景
眾所周知，Apriori算法 在產生頻繁模式完全集前需要對資料庫進行多次掃描，同時產生大量的候選頻繁集，這就使Apriori算法時間和空間複雜度較大。但是Apriori算法中有一個很重要的性質：頻繁項集的所有非空子集都必須也是頻繁的。但是Apriori算法在挖掘額長頻繁模式的時候性能往往低下，Jiawei Han提出了FP-Growth算法 。
預備知識
FP-Tree：將事務數據表中的各個事務數據項按照支持度排序後，把每個事務中的數據項按降序依次插入到一棵以 NULL為根結點的樹中，同時在每個結點處記錄該結點出現的支持度。
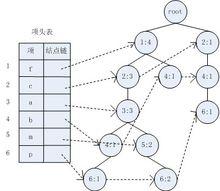FP-Tree結構圖條件模式基：包含FP-Tree中與後綴模式一起出現的前綴路徑的集合
條件樹：將條件模式基按照FP-Tree的構造原則形成的一個新的FP-Tree
算法思想
基本思路：不斷地疊代FP-tree 的構造和投影過程
算法描述如下：
1、對於每個頻繁項，構造它的條件投影資料庫和投影FP-tree。
2、對每個新構建的FP-tree重複這個過程，直到構造的新FP-tree為空，或者只包含一條路徑。
3、當構造的FP-tree為空時，其前綴即為頻繁模式；當只包含一條路徑時，通過枚舉所有可能組合併與此樹的前綴連線即可得到頻繁模式。
算法描述
構造FP-Tree
挖掘頻繁模式前首先要構造FP-Tree，算法偽碼如下：
輸入:一個交易資料庫DB和一個最小支持度threshold.
輸出:它的FP-tree.
步驟:
1.掃描資料庫DB一遍.得到頻繁項的集合F和每個頻繁項的支持度.把F按支持度遞降排序,結果記為L.
2.創建FP-tree的根節點,記為T,並且標記為’null’.然後對DB中的每個事務Trans做如下的步驟.
根據L中的順序,選出並排序Trans中的事務項.把Trans中排好序的事務項列表記為[p|P],其中p是第一個元素,P是列表的剩餘部分.調用insert_tree([p|P],T).
函式insert_tree([p|P],T)的運行如下.
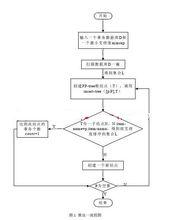FP-Tree創建的算法流程圖如果T有一個子結點N,其中N.item-name=p.item-name,則將N的count域值增加1;否則,創建一個新節點N,使它的count為1,使它的父節點為T,並且使它的node_link和那些具有相同item_name域串起來.如果P非空,則遞歸調用insert_tree(P,N).
註：構造FP-Tree的算法理解上相對簡單，所以不過多描述
挖掘頻繁模式
對FP-Tree進行挖掘，算法如下：
輸入:一棵用算法一建立的樹Tree
輸出:所有的頻繁集
步驟:
調用FP-growth(Tree,null).
procedure FP-Growth ( Tree, x)
{
(1) if (Tree只包含單路徑P) then
(2) 對路徑P中節點的每個組合（記為B）
(3) 生成模式B並x，支持數=B中所有節點的最小支持度
(4) else 對Tree頭上的每個ai， do
{
(5) 生成模式B= ai 並 x，支持度=ai.support；
(6) 構造B的條件模式庫和B的條件FP樹TreeB；
(7) if TreeB != 空集
(8) then call FP-Growth ( TreeB , B )
}
}
演示圖
下圖給出了整個算法的演示過程：
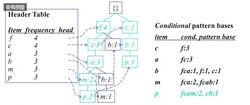FP-Growth算法實例演示圖