算法原理
無論在訓練和建立模板階段還是在識別階段,都先採用端點算法確定語音的起點和終點。以存入模板庫的各個詞條稱為參考模板,一個參考模板可表示為R={R(1),R(2),……,R(m),……,R(M)},m為訓練語音幀的時序標號,m=1為起點語音幀,m=M為終點語音幀,因此M為該模板所包含的語音幀總數,R(m)為第m幀的語音特徵矢量。所要識別的一個輸入詞條語音稱為測試模板,可表示為T={T(1),T(2),……,T(n),……,T(N)},n為測試語音幀的時序標號,n=1為起點語音幀,n=N為終點語音幀,因此N為該模板所包含的語音幀總數,T(n)為第n幀的語音特徵矢量。參考模板與測試模板一般採用相同類型的特徵矢量(如MFCC,LPC係數)、相同的幀長、相同的窗函式和相同的幀移。
假設測試和參考模板分別用T和R表示,為了比較它們之間的相似度,可以計算它們之間的距離 D[T,R],距離越小則相似度越高。為了計算這一失真距離,應從T和R中各個對應幀之間的距離算起。設n和m分別是T和R中任意選擇的幀號,d[T(n),R(m)]表示這兩幀特徵矢量之間的距離。距離函式取決於實際採用的距離度量,在DTW算法中通常採用歐氏距離。
若N=M則可以直接計算,否則要考慮將T(n)和R(m)對齊。對齊可以採用線性擴張的方法,如果N<M可以將T線性映射為一個M幀的序列,再計算它與{R(1),R(2),……,R(M)}之間的距離。但是這樣的計算沒有考慮到語音中各個段在不同情況下的持續時間會產生或長或短的變化,因此識別效果不可能最佳。因此更多的是採用動態規劃(DP)的方法。
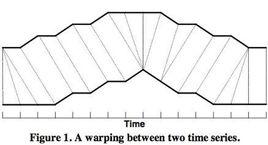
若把測試模板的各個幀號n=1~N在一個二維直角坐標系中的橫軸上標出,把參考模板的各幀號m=1~M在縱軸上標出,通過這些表示幀號的整數坐標畫出一些縱橫線即可形成一個網路,網路中的每一個交叉點(n,m)表示測試模式中某一幀的交匯點。DP算法可以歸結為尋找一條通過此網路中若干格點的路徑,路徑通過的格點即為測試和參考模板中進行計算的幀號。路徑不是隨意選擇的,首先任何一種語音的發音快慢都有可能變化,但是其各部分的先後次序不可能改變,因此所選的路徑必定是從左下角出發,在右上角結束
為了描述這條路徑,假設路徑通過的所有格點依次為(n ,m ),……,(n ,m ),……,(n ,m ),其中(n ,m )=(1,1),(n ,m )=(N,M)。路徑可以用函式m = Oslash;(n )描述,其中n =i,i=1,2,……,N,Ø(1)=1,Ø(N)=M。為了使路徑不至於過傾斜,可以約束斜率在0.5~2的範圍內,如果路徑已經通過了格點(n ,m ),那么下一個通過的格點(n ,m )只可能是下列三種情況之一:
(n ,m )=(n +1,m)
(n ,m )=(n +1,m +1)
(n ,m )=(n ,m+1 )
用r表示上述三個約束條件。求最佳路徑的問題可以歸結為滿足約束條件r時,求最佳路徑函式m =Ø(n ),使得沿路徑的積累距離達到最小值,即:
搜尋該路徑的方法如下:搜尋從(n, m)點出發,可以展開若干條滿足ŋ的路徑,假設可計算每條路徑達到(n, m)點時的總的積累距離,具有最小累積距離者即為最佳路徑。易於證明,限定範圍的任一格點(n, m)只可能有一條搜尋路徑通過。對於(n, m),其可達到該格點的前一個格點只可能是(n-1, m)、(n-1, m -1)和(n, m-1),那么(n, m)一定選擇這3個距離之路徑延伸而通過(n, m),這時此路徑的積累距離為:
D[(n, m)]=d[T(n),R(m)]+min{D(n-1,m),D(n-1,m-1),D(n,m-1)}
這樣可以從(n ,m )=(1,1)出發搜尋(n ,m ),對每一個(n ,m )都存儲相應的距離,這個距離是當前格點的匹配距離與前一個累計距離最小的格點(按照設定的斜率在三個格點中進行比較)。搜尋到(n ,m )時,只保留一條最佳路徑。如果有必要的話,通過逐點向前尋找就可以求得整條路徑。這套DP算法便是DTW算法。
DTW算法可以直接按上面描述來實現,即分配兩個N×M的矩陣,分別為積累距離矩陣D和幀匹配距離矩陣d,其中幀匹配距離矩陣d(i,j)的值為測試模板的第i幀與參考模板的第j幀間的距離。D(N,M)即為最佳匹配路徑所對應的匹配距離
算法比較
DTW算法由於沒有一個有效地用統計方法進行訓練的框架,也不容易將低層和頂層的各種知識用到語音識別算法中,因此在解決大辭彙量、連續語音、非特定人語音識別問題時較之HMM算法相形見絀。HMM是一種用參數表示的,用於描述隨機過程統計特性的機率模型。而對於孤立詞識別,HMM算法和DTW算法在相同條件下,識別效果相差不大, 又由於DTW算法本身既簡單又有效,但HMM算法要複雜得多。它需要在訓練階段提供大量的語音數據,通過反覆計算才能得到參數模型,而DTW算法的訓練中幾乎不需要額外的計算。
程式實現
DTW的一般算法
實現DTW算法的函式Dtw.m
function dist = dtw(t,r)
n=size(t,2);
m=size(r,2);
%%幀匹配距離矩陣
d=zeros(n,m);
fori=1:n
forj=1:m
d(i,j)=(t(i)-r(j)).^2;
end
end
%%累積距離矩陣
D=ones(n,m)*realmax;
%%動態規劃
fori=1:n
forj=1:m
ifi==1&&j==1;
D(i,j)=d(1,1);
D1=0;
D2=0;
D3=0;
end
ifi==1&&j>1
D1=D(i,j-1);
D2=realmax;
D3=realmax;
end
ifj==1&&i>1
D1=D(i-1,j);
D2=realmax;
D3=realmax;
end
ifi>1&&j>1
D1=D(i-1,j);
D2=D(i,j-1);
D3=D(i-1,j-1);
end
D(i,j)=d(i,j)+min([D1,D2,D3]);
end
end
dist=D(n,m);
程式中,首先申請兩個n×m的距陣D和d,分別為累積距離和幀匹配距離。這裡n和m為測試模板與參考模板的幀數。然後通過一個循環計算兩個模板的幀匹配距離距陣d。接下來進行動態規劃,為每個格點(i,j)都計算其三個可能的前續格點的累積距離D1、D2和D3。考慮到邊界問題,有些前續格點可能不存在,因此要加入一些判斷條件。
最後利用最小值函式min,找到三個前續格點的累積距離的最小值作為累積距離,與當前幀的匹配距離d(i,j)相加,作為當前格點的累積距離。該計算過程一直達到格點(n,m),並將D(n,m)輸出,作為模板匹配的結果。
使用原因
孤立詞識別方案主要有:
(1)採用動態規劃(Dynamic Programming)的方法。這是一種運算量較大,但技術上較簡單,正識率也較高的方法。其中的失真測度可以用歐氏距離(適於短時譜或倒譜參數),也可以用對數似然比距離(適於LPC參數).決策方法可用最近鄰域準則.
(2)採用矢量量化(Vector Quantization)的方法.它既可用於語音通信中的波形或參數的壓縮,也可用於語音識別.尤其有限狀態矢量量化(FSVQJ)方法,對於語音識別更為有效。決策方法一般用最小平均失真準則。
(3)採用隱馬爾柯夫模型(HMM)的方法,該模型的參數既可以用離散機率分布函式,也可以用最新的連續機率密度函式(如:正態高斯密度,高斯自回歸密度等)。決策方法則用最大後驗機率準則.
(4)採用混合技術的方法。例如:用矢量量化作為第一級識別(作為預處理,從而得出若干候選的識別結果),然後,再用DTW或HMM方法做最後的識別,因此,可有VQ(矢量化)/DTW和VQ/HMM等識別方法.
三字碼
四字代碼 三字碼 機場名稱 國家省/地區 KDTW DTW 底特律 美國密西根州韋恩縣