簡介
第二次超弦革命發生於上世紀九十年代中期, 通過對非微擾弦理論的研究,人們對弦理論的結構,內部自洽性等有了更深刻的理解,這中間起著決定作用的是弦對偶的概念。通過各種對偶關係, 五種相互獨立的微擾弦理論可以聯繫起來,並可以被看作一個統一理論在不同的背景下的展開。非微擾物理指的是不能通過微擾展開來研究的效應。在通常的量子場論中,非微擾效應如孤立子,瞬子等已被證明對理論的研究非常重要。同樣,在弦理論中一個被稱為D-膜的非微擾孤立子也是理解弦理論本質的關鍵。
Dp-膜是一個(p+1)維的世介面(p維空間加1維時間),開弦端點在其上可以自由地移動。實際上,對開弦的研究發現,它的端點必須在D-膜上。端點在D-膜上的開弦的無質量激發描述D-膜的振動,所以D-膜的開弦描述在低能下是一個有效規範場論。
上面的討論中我們忽視了一個重要的事實,即膜位形可能是不穩定的。不穩定的膜位形在弦理論中大量存在,而且過去幾年對不穩定的膜位形的研究被證明是極有價值的,大大拓寬了我們對D-膜和非微擾弦理論的認識。不穩定的膜位形指的是其振動譜中包含有質量平方為負的快子,快子的存在說明位形是不穩定的。快子凝聚使不穩定的膜位形衰變到一個穩定的位形,通常是一個穩定的膜位形。描述不穩定的膜位元形物理的一個有效而重要的工具就是開弦場論。
另一方面,儘管人們認識到在五種微擾弦理論背後存在著一個統一的理論,但對其知之甚微。僅僅瞭解理論在不同背景下的微擾性質是遠遠不夠的,要定義一個完整的理論,我們需要知道非微擾的物理,況且為了瞭解我們所處的世界,我們需要對這個統一理論的動力學有一個完整的知識,解決問題的一個可能是每一個微擾弦理論都有一個弦場論,從而有了一個非微擾的定義,不同的弦對偶對應於一個理論通過變數變換到另一個理論。
相關資料
20世紀的物理學有兩次大的革命:一次是狹義相對論和廣義相對論,它幾乎是愛因斯坦一人完成的;另一次是量子理論的建立。經過人們的努力,量子理論與狹義相對論成功地結合成量子場論,這是迄今為止最為成功的理論。粒子物理的標準模型理論預言電子的磁矩和實驗給出的數值在誤差是完全一致的,精確度達13位有效數值。廣義相對論也有長足的發展,在小至太陽系,大至整個宇宙範圍里,實驗觀測與理論很好地符合。但在極端條件下,引出了時空奇異,顯示了理論自身的不完善。就我們現在的認識水平,量子場論和廣義相對論是相互不自洽的,因此量子場論和廣義相對論應該在一個更大的理論框架里統一起來。現在這一更大的理論框架已初顯端倪,它就是超弦理論。
超弦理論是物理學家追求統一理論的最自然的結果。愛因斯坦建立相對論之後自然地想到要統一當時公知的兩種相互作用--萬有引力和電磁力。他花費了後半生近40年的主要精力去尋求和建立一個統一理論,但沒有成功。現在回過頭來看歷史,愛因斯坦的失敗並不奇怪。實際上自然界還存在另外兩種相互作用力--弱力和強力。現在已經知道,自然界中總共4種相互作用力除有引力之外的3種都可有量子理論來描述,電磁、弱和強相互作用力的形成是用假設相互交換“量子”來解釋的。但是,引力的形成完全是另一回事,愛因斯坦的廣義相對論是用物質影響空間的幾何性質來解釋引力的。在這一圖像中,瀰漫在空間中的物質使空間彎曲了,而彎曲的空間決定粒子的運動。人們也可以模仿解釋電磁力的方法來解釋引力,這時物質交換的“量子”稱為引力子,但這一嘗試卻遇到了原則上的困難--量子化後的廣義相對論是不可重整的,因此,量子化和廣義相對論是相互不自洽的。
超弦理論是人們拋棄了基本粒子是點粒子的假設而代之以基本粒子是一維弦的假設而建立起來的自洽的理論,自然界中的各種不同粒子都是一維弦的不同振動模式。與以往量子場論和規範理論不同的是,超弦理論要求引力存在,也要求規範原理和超對稱。毫無疑問,將引力和其他由規範場引起的相互作用力自然地統一起來是超弦理論最吸引人的特點之一。因此,從1984年底開始,當人們認識到超弦理論可以給出一個包容標準模型的統一理論之後,一大批才華橫溢的年輕人自然地投身到超弦理論的研究中去了。
經過人們的研究發現,在十維空間中,實際上有5種自洽的超弦理論,它們分別是兩個IIA和IIB,一個規範為Apin(32)/Z2的雜化弦理論,一個規範群為E8×E8的雜化弦理論和一個規範為SO(32)的I型弦理論。對一個統一理論來說,5種可能性還是稍嫌多了一些。因此,過去一直有一些從更一般的理論導出這些超弦理論的嘗試,但直到1995年人們才得到一個比較完美的關於這5種超弦理論統一的圖像。
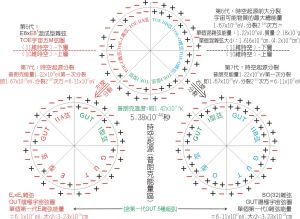
這一圖像可以有用上圖來表示。存在一個唯一的理論,姑且稱其為M理論。M理論有一個很大的模空間(各種可能的真空構成的空間)。5種已知的超弦理論和十一維超引力都是M理論的某些極限區域或是模空間的邊界點(圖中的尖點)。有關超弦對偶性的研究告訴我們,沒有模空間中的哪一區域是有別於其他區域而顯得更為重要和基本的,每一區域都僅僅是能較好地描述M理論的一部分性質。但是,在將這些不同的描述自洽地柔合起來的過程中我閃也學到了對偶性和M理論的許多奇妙性質,尤其是各種D-膜相互轉換的性質。
在此我們不得不提到超弦理論成功地解釋了黑洞的熵和輻射,這是第一次從微觀理論出發,利用統計物理和量子力學的基本原理,嚴格了導出了巨觀物體黑洞的熵和輻射公式,毫無疑問地確立了超弦理論是一個關於引力和其他相互作用力的正確理論。
將5種超弦理論和十一維超引力統一到M理論無疑是成功的,但同是也向人們提出了更大的挑戰。M理論在提出時並沒有一個嚴格的數學表述,因此尋找M理論的數學表述和仔細研究M理論的性質就成了這一時期理論物理研究熱點。
道格拉斯(Douglas,MR)等人仔細研究了D-膜的性質,發現了在極短距離下,D-膜間的相互作用可以完全由規範理論來描述,這些相互作用也包括引力相互作用。因此,極短距離下的引力相互作用實際上是規範理論的量子效應。基於這些結果,班克(Banks,T)等人提出了用零維D-膜(也稱點D-膜)作為基本自由度的M理論的一種基本表述--矩陣理論。
矩陣理論是M理論的非微擾的拉氏量表述,這一表述要求選取光錐坐標系和真空背景至少有6個漸近平坦的方向。利用這一表述已經證明了許多偶性猜測,得到了一類新的沒有引力相互作用的具有洛侖茲不變的理論。如果我們將注意力放在能量為1/N量級的態(N為矩陣的行數或列數),在N趨於無窮大的極限下,可以導出一類通常的規範場理論。許多跡象表明,在大N極限下,理論將變得更簡單,許多有限N下的自由度將不與物理的自由度耦合,因而可以完全忽略。所有這些結論都是在光錐坐標系和有限N下得到的,可以預期一個明顯洛侖茲不變的表述將是研究上述問題極有力的工具。具體來說,人們期望在如下問題的研究上取得進展:
(1)全同粒子的統計規範對稱性應從一個更大的連續的規範對稱性導出。
(2)時空的存在應與超對稱理論中玻色子和費米子貢獻相消相關聯。
(3)當我們緊緻化更多維數時,理論中將出現更多的自由度,如何從量子場論的觀點理解這一奇怪的性質?
(4)有效引力理論的短距離(紫外)發散實際上是某些略去的自由度的紅外發散,這些自由度對應於延伸在兩粒子間的一維D-膜,從場論的觀點來看,這此自由度的性質是非常奇怪的。
(5)將M理論與宇宙學聯繫起來。
顯然,沒有太多的理由認為矩陣理論是M理論的一個完美的表述。值得注意的是矩陣理論的確給出了許多有意義的結果,因此也必定有其物理上合理的成分,這很像本世紀初量子力學完全建立前的時期(那時,普良克提出能量量子導出黑體輻射公式,玻爾提出軌道量子化給出氫原子光譜),一些有關一個全新理論的跡象和物理內涵已經被人們發現了。但是,我們離真正建立一個完美自洽M理論還相距甚遠,因此有必要從超弦理論出發更多更深地發掘其內涵。在這方面,超弦理論的研究又有了新的突破。
1997年底,馬爾達塞納(Maldacena)基於D-膜的近視界幾何的研究發現,緊化在AdS5×S5上的IIB型超弦理論與大N SU(N)超對稱規範理論是對偶的,有望解決強耦合規範場論方面一些基本問題如夸克禁閉和手征對稱破缺。早在70年代,特胡夫特(´t Hooft)就提出:在大N情況下,規範場論中的平面費曼圖將給出主要貢獻,從這一結論出發,波利考夫(Polyakov)早就猜測大N規範場論可以用(非臨界)弦理論來描述,現在馬爾塞納的發現將理論和規範理論更加具體化了。1968年維內齊諾(Veneziano)為了解決相互作用而提出了弦理論,發現弦理論是一個可以用來統一四種相互作用力的統一理論,對偶性的研究引出了M理論,現在馬爾達塞納的研究又將M理論和超弦理論與規範理論(可以用來描敘強相互作用)聯繫起來,從某種意義上來說,我們又回到了強相互作用的這一點,顯然我們對強相互作用的認識有了極大的提高,但是我們仍沒有完全解決強相互作用的問題,也沒有解決四種相互作用力的統一問題,因此對M理論、超弦理論和規範理論的研究仍是一個長期和非常困難的問題。