Introduction Of Family
In the history of science, scientists and son, brother, it's not uncommon for scientists, however, in a family of several generations, many scientists of the brother and son are relatively rare, as Swiss of the Bernoulli family is a prominent In the history of science, scientists and son, brother, it's not uncommon for scientists, however, in a family of several generations, many scientists of the brother and son are relatively rare, as Swiss of the Bernoulli family is a prominent . Bernoulli family 3 generation are 8 bit scientists, distinguished, at least three; and this generation of numerous sons, at least half of the Bernoulli family became prominent members of the Bernoulli family 3 generation are 8 bit scientists, distinguished, at least three; and this generation of numerous sons, at least half of the Bernoulli family became prominent members of the .
there was a descendant of not less than 120 bits are systematically over - traced, mathematics, science, technology, engineering and law, management, literature, art and fame, there was a descendant of not less than 120 bits are systematically over - traced, mathematics, science, technology, engineering and law, management, literature, art and fame,. became so famous that even the most incredible is this family has two generations, most mathematicians, did not intentionally chose mathematics as a profession, yet soulful indulging a taste for mathematics, with allegations that they're like the drunkard met spirits became so famous that even the most incredible is this family has two generations, most mathematicians, did not intentionally chose mathematics as a profession, yet soulful indulging a taste for mathematics, with allegations that they're like the drunkard met spirits .
old Nicolas Bernoulli (Nicolaus Bernoulli, 1623 AD - 1708) was born in Basel, well - educated, had worked in local government and the judiciary as a senior job old Nicolas Bernoulli (Nicolaus Bernoulli, 1623 AD - 1708) was born in Basel, well - educated, had worked in local government and the judiciary as a senior job . 3 He has the golden boy, the son of the eldest son of Jacob ( 3 He has the golden boy, the son of the eldest son of Jacob (.
wherein,A.D. 1654 - 1705) and the third son of John (Johann, AD 1667 - 1748) to become the famous mathematician, the second son (Nicholas, Nicolaus I, 1662 - 1716 A.D.) in St. Petersburg Academy of Sciences and became a member of the mathematics before, is Bern's first Professor of Law 
Jacob
December 27, 1654, Jacob Bernoulli was born in Basel, is a graduate of the University of Basel, in 1671 at the age of 17 was awarded a Master of Arts in Art December 27, 1654, Jacob Bernoulli was born in Basel, is a graduate of the University of Basel, in 1671 at the age of 17 was awarded a Master of Arts in Art . here means the "liberal arts", including arithmetic, geometry, astronomy, mathematics and music and grammar, rhetoric, oratory, belonging to 7 phyla here means the "liberal arts", including arithmetic, geometry, astronomy, mathematics and music and grammar, rhetoric, oratory, belonging to 7 phyla .
on his father's wishes, he was 22 years old when he was made Master on his father's wishes, he was 22 years old when he was made Master . however, he is also contrary to the will of the father, and taught himself mathematics and astronomy however, he is also contrary to the will of the father, and taught himself mathematics and astronomy .
in 1676, he arrived in Geneva as a tutor of in 1676, he arrived in Geneva as a tutor of . from 1677 onwards,He began to write rich content there of "Meditations," from 1677 onwards,He began to write rich content there of "Meditations," .
1678 and 1681, Jacob Bernoulli twice to travel and study, been to France, the Netherlands, Britain and Germany, contacts and exchanges have been alfred, Boyle, Hooker, scientists such as Huygens wrote about comet theory (1682), a theory of gravity (1683) the aspects of scientific and technological articles 1678 and 1681, Jacob Bernoulli twice to travel and study, been to France, the Netherlands, Britain and Germany, contacts and exchanges have been alfred, Boyle, Hooker, scientists such as Huygens wrote about comet theory (1682), a theory of gravity (1683) the aspects of scientific and technological articles . 1687, Jacob in "The Journal" published a treatise on Mathematics for two mutually perpendicular straight lines in the area of the triangle by quartering method ", the same year became professor of mathematics at the University of Basel,until 1705 on Aug. 16, 2010
died in 1699, Jacob was elected a foreign member of the Academy of Sciences in Paris; Berlin Scientific Society in 1701 (and later by the Berlin Academy of Sciences) for admission to membership died in 1699, Jacob was elected a foreign member of the Academy of Sciences in Paris; Berlin Scientific Society in 1701 (and later by the Berlin Academy of Sciences) for admission to membership . many mathematical achievements and Jacob the names associated with the record or field.
For example catenary problems (in 1690), the formula of the radius of curvature (1694), "lemniscate of bernoulli" (1694), "Bernoulli differential equation" (1695), "isoperimetric problem"(1700) and the like For example catenary problems (in 1690), the formula of the radius of curvature (1694), "lemniscate of bernoulli" (1694), "Bernoulli differential equation" (1695), "isoperimetric problem"(1700) and the like . Jacob mathematics' most important contribution was the development of probability theory in terms of Jacob mathematics' most important contribution was the development of probability theory in terms of .
from 1685 onwards he published in a gambling game win or loss is the question of the number of papers, later wrote in "surmise", the book after his death in 8 years, i.e. in 1713 published two of the most talked - of anecdotes, and Jacob is preoccupied with the logarithmic spiral, the study from published two of the most talked - of anecdotes, and Jacob is preoccupied with the logarithmic spiral, the study from .
began in 1691 he discovered, through various transform of a logarithmic spiral is a logarithmic spiral, as its evolute and involute are logarithmic spirals, from the poles to the tangent of a foot trajectory,to pole for the light - emitting point of the logarithmic spiral is obtained after reflected by the reflection, and with all these reflection lines tangent to the curve (return light) are logarithmic spirals began in 1691 he discovered, through various transform of a logarithmic spiral is a logarithmic spiral, as its evolute and involute are logarithmic spirals, from the poles to the tangent of a foot trajectory,to pole for the light - emitting point of the logarithmic spiral is obtained after reflected by the reflection, and with all these reflection lines tangent to the curve (return light) are logarithmic spirals . admitting this curve of magic in his will, that posterity will require logarithmic spiral engraved on his tombstone, to the mantra "Never change, keeping the circumstances unchanged", to symbolize immortality after death admitting this curve of magic in his will, that posterity will require logarithmic spiral engraved on his tombstone, to the mantra "Never change, keeping the circumstances unchanged", to symbolize immortality after death .
Bernoulli Number
B (0) = 1, B) = (1 - 1 / 2, B (2) = 1 / 6, B = 0 (3), (B) = 1 / 4 - 30, B = 0 (5), 6 (B) = 1 / 42, B = 0 (7), (B) = 8 / 1 - 30, B = 0) (9), 10 (B) = 5 / 66, B) = 0 (11, 12 (B) = - 691 / 2730, B) = 0 (13, 14 (B) = 7 / 6, B = 0 (15), 16 (B) = - 3617 / 510, B = 0 (17), (B) = 18 / 43867 798, B (18) = 0, B) = (20 - 330 / 174611.. in general, n = 1, B (2n + 1) = 0; n = 2, has the formula B (n) = C (k, n) * B (k) (k: 0 - n) may be used to calculate Bernoulli numbers by Bernoulli? in number theory is very useful for the record or field.
For example, Huppert equation - - = 4 (= 1 (mod4) are primes, N. C. Ankeny and E. Ah, had to guess what the minimum solution (x0 + y0) * (p) is satisfied, in 1960,Excusing = 37, 59, 67, and the rest of the primes are all regular primes Therefore, Fermat's theorem, Kummer's result is groundbreaking work (see equation in the Therefore, Fermat's theorem, Kummer's result is groundbreaking work (see equation in the .
), though there are many primes of formal discrimination laws, however, whether there are infinitely many regular primes, unresolved ), though there are many primes of formal discrimination laws, however, whether there are infinitely many regular primes, unresolved . informal but there are infinitely many primes, as early as 1915, 'as he is proven by the fact that informal but there are infinitely many primes, as early as 1915, 'as he is proven by the fact that .
John
Jacob Bernoulli's younger brother John Bernoulli than small 13 - year - old brother, 1667 / 8 / 6 and was born in Basel, on 1 January 1748 and died in Basel, aged 81, and brother, he is only 51 years old Jacob Bernoulli's younger brother John Bernoulli than small 13 - year - old brother, 1667 / 8 / 6 and was born in Basel, on 1 January 1748 and died in Basel, aged 81, and brother, he is only 51 years old . John 1685 to 18 years old when awarded his Master of Arts at the University of Basel, with his brother Jacob John 1685 to 18 years old when awarded his Master of Arts at the University of Basel, with his brother Jacob .
as their father was old and his oldest son Jacob Nicholas to study law, a son, John, to engage in family management transaction but as their father was old and his oldest son Jacob Nicholas to study law, a son, John, to engage in family management transaction but . John Jacob must under the leadership of the revolt, and to study medicine and classics John Jacob must under the leadership of the revolt, and to study medicine and classics .
John 1690 obtained the degree of medical master graduates,In 1694 and also holds a PhD in John 1690 obtained the degree of medical master graduates,In 1694 and also holds a PhD in . but he found his interest mathematics he is but he found his interest mathematics he is .
Jacob learning maths, and knows a lot about the Jacob learning maths, and knows a lot about the . in 1695, the 28 - year - old John made his first academic position at Professor of Mathematics at the University of Groningen in the Netherlands in 1695, the 28 - year - old John made his first academic position at Professor of Mathematics at the University of Groningen in the Netherlands .
10 years later (1705), replacing John Jacobs died of Basel University mathematics professor Ren 10 years later (1705), replacing John Jacobs died of Basel University mathematics professor Ren . with his brother, he was also elected to the Paris Academy of Sciences and foreign member of the Berlin Science Association with his brother, he was also elected to the Paris Academy of Sciences and foreign member of the Berlin Science Association .
1712, 1724 and 1725, he also was elected a fellow of the Royal Society,Italy's Bologna Academy of Sciences and Saint Petersburg Academy of Sciences and foreign member of the 1712, 1724 and 1725, he also was elected a fellow of the Royal Society,Italy's Bologna Academy of Sciences and Saint Petersburg Academy of Sciences and foreign member of the . John Jacob of mathematics achievement than more John Jacob of mathematics achievement than more .
e.g. solving problems of a catenary line (1691), proposed using L 'Hospitol principle (1694), the brachistochrone (1696) and the geodesic problem (1697), gives a definite integral by variable substitution (1699), study the problem of vibrations of the strings (1727), who published "Continuity, tutorial" (1742) and John with his contemporaries of the bit 110 in correspondence with scholars, academic discussion of the letters are about 2500,many of them becoming precious science literature, e.g. with his brother Jacob, and Leibniz, Huygens and others on the catenary, the brachistochrone (i.e., line) and the problem's communication is discussed, although debate continued, especially John and Jacob accused the vitriolic attacks they face each other, so that between the brothers often cause unpleasant, but the debate will undoubtedly promote the development of science, the brachistochrone problem has led to the birth of the calculus of
John another feat, and developed a large number of outstanding mathematicians, including 18th century most of the famous mathematician Euler, a Swiss mathematician Clem, French mathematician L ',- and his own son, Daniel, and nephew of Nicholas II such as John another feat, and developed a large number of outstanding mathematicians, including 18th century most of the famous mathematician Euler, a Swiss mathematician Clem, French mathematician L ',- and his own son, Daniel, and nephew of Nicholas II such as .
Daniel
Step2:
Daniel Bernoulli, Daniel Bernoulli (1700 ~ 1782) Swiss physicist, mathematician, scientist Daniel Bernoulli, Daniel Bernoulli (1700 ~ 1782) Swiss physicist, mathematician, scientist . 1700 was born on February 8, Groningen, The Netherlands 1700 was born on February 8, Groningen, The Netherlands .
the Bernoulli family in the most famous of a distinguished mathematician he is the Bernoulli family in the most famous of a distinguished mathematician he is . J. Bernoulli's second son, and his father, contrary to the wishes of his parents to do business, to study medicine, he worked in the Berg, Lester thinking Fort and Basel universities such as the study of philosophy, ethics,In 1721 acquires medical
. Nourrit's degree by age 25 (1725) in St. Petersburg Academy of Sciences of the University of Mathematics Fellow
8 years later returned to Basel in Switzerland, served as the first professor of anatomy, dynamics, he was appointed professor, in 1750 and became a professor of physics at 8 years later returned to Basel in Switzerland, served as the first professor of anatomy, dynamics, he was appointed professor, in 1750 and became a professor of physics at . 1725 - 1749 years, Bernoulli was ten times of the French Academy of Sciences awarded the annual prize, 1725 - 1749 years, Bernoulli was ten times of the French Academy of Sciences awarded the annual prize, .
1782 on March 17, Bernoulli in Basel, Switzerland, died at the age of 82 1782 on March 17, Bernoulli in Basel, Switzerland, died at the age of 82 .
Personal Experiences
John Bernoulli wanted to force his second son went into business with Daniel but Daniel stuck off the cuff in mathematics before he chose to become a doctor or a medical John Bernoulli wanted to force his second son went into business with Daniel but Daniel stuck off the cuff in mathematics before he chose to become a doctor or a medical . Daniel, 1700 ~ 1782) was born in Groningen, in 1716 at age 16 and was awarded a Master of Arts; in 1721 and gained a Medical Doctor Daniel, 1700 ~ 1782) was born in Groningen, in 1716 at age 16 and was awarded a Master of Arts; in 1721 and gained a Medical Doctor .
he had applied for the post of professor of botany and anatomy, but not successful he had applied for the post of professor of botany and anatomy, but not successful . Daniel by fathers influence. I always like mathematics
in 1724, his journey was published in Venice in the "mathematical exercise", attracted academic attention,to be invited to participate in the St. Petersburg Academy of Sciences work the same year, he also solved the differential equation with variable separation in the Riccati equation of the same year, he also solved the differential equation with variable separation in the Riccati equation of .
1725, 25 - year - old Daniel was appointed as professor of mathematics at 1725, 25 - year - old Daniel was appointed as professor of mathematics at . St. Petersburg in 1727, the 20 - year - old (later generations titled him with Euler Archimedes, Isaac Newton and Gauss was ranked as one of the "Four Men"), St. Petersburg to become assistant to Daniel
however, it is important to place in the life of St. Petersburg of vulgarity to my aid, so eight years later in 1733, he found an opportunity of returning to Basel, where he eventually became professor of botany and anatomy,Finally he became head of a physics professor at in 1734, Daniel won the Paris Academy of Sciences prize, after 10 times of the bonus in 1734, Daniel won the Paris Academy of Sciences prize, after 10 times of the bonus .
Daniel comparable only with the great mathematician Euler and Euler Daniel comparable only with the great mathematician Euler and Euler . Daniel kept for nearly 40 years of scholarly communication, science is a Daniel kept for nearly 40 years of scholarly communication, science is a .
in the Bernoulli family, Daniel is involved in scientific fields, including the city of in the Bernoulli family, Daniel is involved in scientific fields, including the city of . he wrote a classic "fluid dynamics" (1738); study on the elastic string lateral vibration (1741 - 1743),proposed the propagation of sound in air law (1762) he wrote a classic "fluid dynamics" (1738); study on the elastic string lateral vibration (1741 - 1743),proposed the propagation of sound in air law (1762) .
his treatise also deals with astronomy (in 1734), gravity (1728), Lake (Xi) in 1740, 1743, 1746), the vibration theory (1747), the hull of the sail is stable (1753, 1757) and physiology (1721), etc.) in 1728 Vanier became knowledgeable of the Bernoulli family of representative Vanier became knowledgeable of the Bernoulli family of representative .
Daniel to 1747 he was elected Academician of the Academy of Berlin, and in 1748 was elected academician of the Academy of Paris,Membership of the Royal Society elected in 1750, Daniel to 1747 he was elected Academician of the Academy of Berlin, and in 1748 was elected academician of the Academy of Paris,Membership of the Royal Society elected in 1750, . he has won several honorary titles of he has won several honorary titles of .
Scientific Achievements
1. In physics of contribution are as follows: (1) the publication in 1738 of "fluid dynamics", which played a total of 13: This is his most important work This is his most important work .
that used the energy conservation law to solve the problem of fluid flow, and wrote the basic equations of fluid dynamics, to be called" Bernoulli equation is put forward to increase the flow rate of pressure reduction "of the Bernoulli principle that used the energy conservation law to solve the problem of fluid flow, and wrote the basic equations of fluid dynamics, to be called" Bernoulli equation is put forward to increase the flow rate of pressure reduction "of the Bernoulli principle . (2) He has also been proposed as a pneumatic pressure to the gas molecules on the surfaces of the container wall by the effect of thermal and kinetic theory basic concept,and kinetic pressure and with temperature increasing strengthening of facts (2) He has also been proposed as a pneumatic pressure to the gas molecules on the surfaces of the container wall by the effect of thermal and kinetic theory basic concept,and kinetic pressure and with temperature increasing strengthening of facts .
(3) from 1728 onwards, he was also the co - study has flexibility and elasticity of chain and girders of mechanical problems, including the objects of the equilibrium curve, it is possible to extend the chord and the vibrations of air column (3) from 1728 onwards, he was also the co - study has flexibility and elasticity of chain and girders of mechanical problems, including the objects of the equilibrium curve, it is possible to extend the chord and the vibrations of air column . (4) for his astronomical measurement, the gravity of the earth and tides, magnetism, ocean currents, the hull of the sail is stable, Saturn and Jupiter's irregular motion and vibration theory achievement award for (4) for his astronomical measurement, the gravity of the earth and tides, magnetism, ocean currents, the hull of the sail is stable, Saturn and Jupiter's irregular motion and vibration theory achievement award for .
2. In mathematics, calculus, differential equations and probability theory, etc, he also has done a lot of important work
Bernoulli Law
In a fluid system, such as air, water, the faster the flow rate, fluid pressure generated is smaller, and this is referred to as" the father of Fluid Mechanics" by Daniel Bernoulli in 1738 - discovered "laws of Bernoulli" In a fluid system, such as air, water, the faster the flow rate, fluid pressure generated is smaller, and this is referred to as" the father of Fluid Mechanics" by Daniel Bernoulli in 1738 - discovered "laws of Bernoulli" . this pressure generated by the power of the air is able to lift a heavy aircraft, took advantage of the Bernoulli law this pressure generated by the power of the air is able to lift a heavy aircraft, took advantage of the Bernoulli law .
of an aircraft wing is smooth on the surface of the curved surface, and defines the lower surface is a plane like this of an aircraft wing is smooth on the surface of the curved surface, and defines the lower surface is a plane like this ., on the wing surface the airflow velocity is greater than the lower surface of the airflow speed, the airflow beneath the wing and generate greater than the pressure above the pressure of the airflow, the aircraft by a tremendous pressure difference between "hold", on the wing surface the airflow velocity is greater than the lower surface of the airflow speed, the airflow beneath the wing and generate greater than the pressure above the pressure of the airflow, the aircraft by a tremendous pressure difference between "hold".
Of course, this pressure have a high aspect of hydromechanics equation "Bernoulli equation" would go on to some it Of course, this pressure have a high aspect of hydromechanics equation "Bernoulli equation" would go on to some it .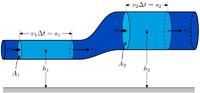
Equation
v = the flow velocity of the Bernoulli law g = the acceleration of the earth (ground) h = height of the fluid is from the reference point (a) p = fluid pressure of the fluid density. rho. =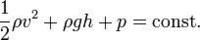
Bernoulli Equation
Bernoulli ideal from either the positive potential in the body under the action of a state of steady motion, the equations of motion (i.e., Euler equations along streamlines) obtained by integrating the expression of conservation of mechanical energy of the fluid motion equation because of the famous Swiss scientists the Bernoulli in 1738. It is put forward. It is named for
for the gravitational field in the homogeneous incompressible fluid, the equation p + gz + (1 / 2) * v ^ 2 = C p p in the formula, p, v equals the pressure of the fluid, density and velocity; and z is the vertical height; and g is the acceleration of gravity for the gravitational field in the homogeneous incompressible fluid, the equation p + gz + (1 / 2) * v ^ 2 = C p p in the formula, p, v equals the pressure of the fluid, density and velocity; and z is the vertical height; and g is the acceleration of gravity . on various type represent the unit volume of the fluid pressure p can,rho g gravitational potential energy and kinetic energy (z - 1 / 2) p * v ^ 2, in the process in motion along a streamline, the sum remains the same, i.e. the total energy conservation but
and the flow line between the total energy (i.e., in the above equation is a constant value) may be different for gas, gravity can be ignored, a simplified equation for the (p + 1 / 2) p * v ^ 2 = constant (p0), respectively referred to as the static pressure, dynamic pressure and total pressure gas, gravity can be ignored, a simplified equation for the (p + 1 / 2) p * v ^ 2 = constant (p0), respectively referred to as the static pressure, dynamic pressure and total pressure .
apparently, in the flow speed increases, the pressure is reduced; the speed is decreased, the pressure is increased; the speed is reduced to zero, the pressure reaches a maximum (theoretically) which should be equal to the total pressure apparently, in the flow speed increases, the pressure is reduced; the speed is decreased, the pressure is increased; the speed is reduced to zero, the pressure reaches a maximum (theoretically) which should be equal to the total pressure . aircraft wing producing lift,lies in the lower speed low while the pressure is large, the pressure on the high speed as well as the pressure is low, and therefore an upward resultant aircraft wing producing lift,lies in the lower speed low while the pressure is large, the pressure on the high speed as well as the pressure is low, and therefore an upward resultant .
According to this equation, the measured fluid based on the total pressure, static pressure, to obtain the speed, becomes a Pitot - tube principle According to this equation, the measured fluid based on the total pressure, static pressure, to obtain the speed, becomes a Pitot - tube principle . in irrotational flow, may also be utilized in the irrotational conditions the integral of the Euler equation to obtain the same result but meaning different, in which case the equation with the constants in the whole flow field are unchanged, which indicates that the streamlines of the fluid on the same total energy, an equation is applicable to the whole field between any two points in in irrotational flow, may also be utilized in the irrotational conditions the integral of the Euler equation to obtain the same result but meaning different, in which case the equation with the constants in the whole flow field are unchanged, which indicates that the streamlines of the fluid on the same total energy, an equation is applicable to the whole field between any two points in .
viscous flow, the viscous frictional force consumes the mechanical energy to generate heat, mechanical energy is not conservation, promote the use of the Bernoulli equation, the item shall be added to the loss of mechanical energy viscous flow, the viscous frictional force consumes the mechanical energy to generate heat, mechanical energy is not conservation, promote the use of the Bernoulli equation, the item shall be added to the loss of mechanical energy.
Bernoulli Effect
In 1726, Bernoulli through numerous experiments and discovered "the surface of the boundary layer effect": the fluid speed increases, the object is in contact with the fluid on the interface of the pressure can be reduced, whereas the pressure would increase In 1726, Bernoulli through numerous experiments and discovered "the surface of the boundary layer effect": the fluid speed increases, the object is in contact with the fluid on the interface of the pressure can be reduced, whereas the pressure would increase . in honor of this university scientists, this finding is referred to as the "Bernoulli effect" in honor of this university scientists, this finding is referred to as the "Bernoulli effect" .
the Bernoulli effect and is suitable for a gas including fluid, the fluid flows at steady state of one of the basic phenomena, reflecting the pressure of the fluid velocity on the relationship between the pressure and flow rate: the higher the flow rate of the fluid is large, the pressure is smaller the smaller the flow rate of the fluid, of greater pressure the Bernoulli effect and is suitable for a gas including fluid, the fluid flows at steady state of one of the basic phenomena, reflecting the pressure of the fluid velocity on the relationship between the pressure and flow rate: the higher the flow rate of the fluid is large, the pressure is smaller the smaller the flow rate of the fluid, of greater pressure . for example, inside a conduit of a stable flow of fluid,In the duct at a different cross - section of the vertical opening of the narrow tubes liquid - column height, demonstrating that the steady flow, the flow rate is larger than a predetermined value, the pressure is low, the flow rate of the small local pressure for example, inside a conduit of a stable flow of fluid,In the duct at a different cross - section of the vertical opening of the narrow tubes liquid - column height, demonstrating that the steady flow, the flow rate is larger than a predetermined value, the pressure is low, the flow rate of the small local pressure .
large. this phenomenon is called "Bernoulli effect" Bernoulli equation: p + 1 / 2pv ^ 2 = C Bernoulli equation: p + 1 / 2pv ^ 2 = C .
in the train on the platform were marked in the train on the platform were marked . safe due to the high - speed train heading for us, close to the train compartment air is entrained for movement, the pressure is reduced, on the platform of the passenger if he is too close to the train, the passenger body that clearly shows that the pressure difference, so that travellers will be attracted to train victim to land - safe due to the high - speed train heading for us, close to the train compartment air is entrained for movement, the pressure is reduced, on the platform of the passenger if he is too close to the train, the passenger body that clearly shows that the pressure difference, so that travellers will be attracted to train victim to land - .
of the Bernoulli Effect Example of application: the wing of an aircraft,sprayer, carburetor of gasoline engine, the rotation of the ball for a ball game in of the Bernoulli Effect Example of application: the wing of an aircraft,sprayer, carburetor of gasoline engine, the rotation of the ball for a ball game in .
Related The Anecdote
The famous Bernoulli family produced many legends and anecdotes The famous Bernoulli family produced many legends and anecdotes . to such a scientific genius yet rude language family, which seems natural to to such a scientific genius yet rude language family, which seems natural to .
one of the legends about Daniel is like this: once in the course of the journey, the young Daniel the same witty chat with strangers, he humbly introduce myself and say: "I'm Daniel Bernoulli one of the legends about Daniel is like this: once in the course of the journey, the young Daniel the same witty chat with strangers, he humbly introduce myself and say: "I'm Daniel Bernoulli ." strangers immediately with scornful look replied: "I would be Isaac Newton!"" strangers immediately with scornful look replied: "I would be Isaac Newton!".

