概述
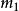BCH循環碼
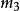BCH循環碼
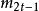BCH循環碼
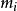BCH循環碼
BCH循環碼若循環碼的生成多項式具有如下形式： g(x)=LCM[(x),(x),…,(x)] 其中LCM表示最低公倍式，t為糾錯個數，(x)為素多項式，則由此生成的循環碼稱為BCH循環碼，其最小碼距d≥=2t+1(d0稱為設計碼距)，它能糾正t個隨機獨立差錯。
循環碼
BCH循環碼
BCH循環碼
BCH循環碼 BCH循環碼 BCH循環碼 BCH循環碼 BCH循環碼具有某種循環特性的線性分組碼，如果(n，κ)線性分組碼Vκ具有如下的性質：對於每一個A=(,，…，)∈Vn，只要∈Vκ，其循環移位亦屬於Vκ，則稱Vκ為循環碼。循環碼的優點在於其編碼和解碼手續比一般線性碼簡單，因而易於在設備上實現。使Vn中的每一個矢量A=(,，…，)，對應於域GF上的多項式ɑ(x)=ɑ+ɑx+…+x。於是Vn中的全體n維矢量便與上述多項式之間建立了一一對應的關係。基於這種對應，使Vn中除了線性運算而外，還建立了矢量之間的乘法運算。A=(,，…，)與B=(b,b,…,)的乘積ab可視為ɑ(x)b(x)[mod(x-1)]所對應的矢量。因此,一個(n,κ)循環碼的生成矩陣及均等校驗矩陣可分別由生成多項式及均等校驗多項式h(x)所代替，從而簡化了編碼及解碼運算。
計算公式
設計距離為9的q元BCH碼的周期分布的計算公式：碼的周期分布為q的冪，當碼的周期不等於某些特殊值時，冪為碼長與周期的最大公因數。當碼的周期為特殊值時，冪為n/b-m[8/b]，這裡n是碼的長度，b是由n和碼的周期決定的2到8之間的整數，m是q模n的指數。由此計算公式和Mobius反轉公式給出了無內周期碼字個數的計數結果。
基本原理
BCH碼是一種有限域中的線性分組碼，具有糾正多個隨機錯誤的能力，通常用於通信和存儲領域中的糾錯編碼。BCH碼定義如下：給定任意一個有限域GF(q)及其擴展域GF(q^m)，其中q是素數或素數的冪，m為正整數。對於任意一個碼元取自擴展域GF(q^m)的循環碼(n,k)，其中n=2^m-1，其生成多項式g(x)具有2t個連續的根{a^1,a^2,a^,...,a^(2t-1),a^(2t)}，則由生成多項式g(x)編碼產生的循環碼稱為q進制的BCH碼，記為(n,k,t)。當碼長n=2^m-1，稱為本原BCH碼，否則稱為非本原BCH碼。
最常用的BCH碼是二進制的BCH碼。二進制BCH碼的所有碼元都是由0和1構成，便於硬體電路的實現。如無說明，本文以下討論的BCH碼都是二進制BCH碼。二進制本原BCH碼具有以下重要參數：
碼長：n=2^m-1
校驗位長度：n-k<=m*t
1.碼長：n=2^m-1
2.校驗位長度：n-k<=m*t
BCH碼的生成多項式是由GF(q^m)的2t個最小多項式最低公倍式的乘積，糾錯能力為t的BCH碼生成多項式為g(x)=LCM{m1(x),m2(x),...,m2t-1(x),m2t(x)}，其中LCM表示最低公倍式，m(x)為最小多項式。
由多項式理論知道，如果有限域GF(2^m)中的元素a^i是m次即約多項式mi(x)的根，則(a^i)^2,(a^i)^4,(a^i)^8,...也是mi(x)的根，(a^i)^2,(a^i)^4,(a^i)^8,...稱為共軛根系。如果兩個根共軛，則它們具有相同的最小多項式。因此生成多項式g(x)=LCM{m(x),m(x),...,m(x),m(x)}=m(x)*m(x)*...*m(x)通過以上步驟就可以求出BCH碼的生成多項式。得到生成多項式就可以對信息進行編碼。
編碼原理
將未編碼的k位數據記為多項式：
m(x)=m+m*x^1+m*x^2+...+m*x^k-1;其中mi屬於{0,1}
將生成多項式記為：
g(x)=g+g*x1+g*x^2+...+g*x^r,其中r=m*t，校驗位記為r(x)，則
r(x)=x^r*m(x) mod g(x)
編碼後的BCH碼字多項式可記為：
C(x)=x^r*m(x)+x^r*m(x) mod g(x)
BCH編碼實現的關鍵是通過除法電路得到校驗位多項式。編碼的過程可總結為：
將m(x)左移r位，得到x^r*m(x)；
用生成多項式g(x)除以x^r*m(x)，得到校驗位多項式r(x)；
得到碼元多項式C(x)=x^r*m(x)+x^r*m(x) mod g(x)。
1.將m(x)左移r位，得到x^r*m(x)；
2.用生成多項式g(x)除以x^r*m(x)，得到校驗位多項式r(x)；
3.得到碼元多項式C(x)=x^r*m(x)+x^r*m(x) mod g(x)。
解碼規則
若秩為 n- κ並且滿足 GH=0，僅當A=( v, v,…， v)∈ n滿足 H=0時，才為 κ中的碼字。稱 H為( n， κ)線性分組碼 κ的均等校驗矩陣，稱 H為矢量的伴隨式。假設 v是傳送的碼矢量，在接收端獲得一個失真的矢量 r= v+ E,式中 E=( e， e，…， e)稱為錯誤型。由此 r H=( v+ e) H= e H
線性碼的解碼原則便以此為基礎。
