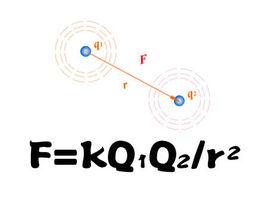
定義
 點電荷
點電荷帶電體的一種理想模型。如果在研究的問題中,帶電體的形狀 、大小以及電荷分布可以忽略不計 ,即可將它看作是一個幾何點,則這樣的帶電體就是點電荷。一個實際的帶電體能否看作點電荷,不僅和帶電體本身有關,還取決於問題的性質和精度的要求。與質點、剛體等概念一樣,點電荷是實際帶電體的抽象和近似,它是建立具有普遍意義的基本規律的不可或缺的理想模型,又是把複雜多樣的實際問題轉化或分解為基本問題時必不可少的分析手段。例如,庫侖定律、洛倫茲力公式的建立,帶電體產生的電場以及帶電體之間相互作用的定量研究,試驗電荷的引入等等,都離不開點電荷 。
實際的帶電體(包括電子、質子等)都有一定大小,都不是點電荷.當電荷間距離大到可認為電荷大小、形狀不起什麼作用時,可把電荷看成點電荷。
理解
就字面上理解,“點電荷”就是帶電體,是一個沒有大小和形狀的幾何點。而電荷又全部集中在這幾何點上。事實上,任何帶電體都有其大小和形狀,真正的點電荷是不存在的,它像力學中的“質點”概念一樣,純屬一個理想化模型。不過,當我們在研究帶電體間的相互作用時,如果帶電體本身的幾何線度比起它們之間的距離小得很多,那么,帶電體的形狀、大小和電荷分布對帶電體之間的相互作用的影響就可以忽略不計。在此情況下,我們仍可以把帶電體抽象成點電荷模型。也只有這樣,“電荷之間的距離”這一概念本身才有完全確定的意義。故從此角度看,點電荷又是一個相對性概念。為了能對點電荷的相對性認識得更充分、更深刻,我們不妨再以均勻帶電圓盤中心軸線上的場強公式為例來加以說明。均勻帶電圓盤軸線上任一點的場強公式為:
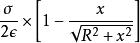 點電荷
點電荷式中ε是真空中的介電常數,σ是圓盤上的電荷面密度,R為圓盤半徑,x是軸線上所論點到圓盤中心的距離。
當R≫x,即對於軸線上所論點看來可以認為均勻帶電圓盤為“無限大”時,所論點的場強等於E=σ/2ε,相當於無限大帶電平面附近的電廠,可看成是均勻場,場強垂直於板面,正負由電荷的符號決定。
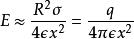 點電荷
點電荷若x≫R,則按二項式定理展開並略去Rx的高冪項,即得:
式中q=σπR 是圓盤所帶電量。由此可見,當圓盤軸線上所論點到圓盤中心的距離與圓盤本身的大小相比為很大時,所論點的場強與帶電量q的圓盤其中心的一個點電荷在該點所產生的場強相同。
這裡特別值得一提的是,點電荷決不像有些人認為的那樣,一定是一個帶有很少電量的帶電體。點電荷可以是電量很小,也可以是電量很大。另外,正像力學中可以把任何物體看作質點的集合一樣,任何帶電體都可以看作是點電荷的集合。由此,若相互作用的不是點電荷而是有限大帶電體,則原則上總可將帶電體看成是由無限個點電荷元所組成的連續點電荷系,然後再利用適用點電荷相互作用規律的庫侖定律,通過求和或積分求出兩帶電體之間的相互作用力。在中學物理中,如果未特別指出帶電體的形狀、大小,則為簡便起見,一般都把此帶電體當作點電荷來處理。
作為一種特殊情況,有時帶電體的大小雖然在研究問題中不能忽略,但帶電體形狀比較規則,具有對稱性,以至電荷分布也具有對稱性。這時,帶電體對外所顯的電特性往往跟一個等效點電荷的電特性相同。於是,我們也可以把此帶電體等效成一個點電荷來處理。譬如,一個有限大均勻帶電的球體,它在球外各點的電場和電勢與一個與其帶等量電荷,位置在其球心的點電荷所產生的電場一模一樣。正因為如此,在求球外任一點的電特性或求兩帶電球體的相互作用力時,我們才把它們均看作是電量全部集中在球心的點電荷。事實證明,這樣處理問題既簡捷又可靠。
計算方法
庫侖定律
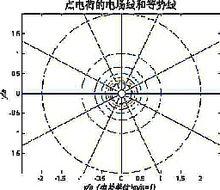 點電荷的電場域和等勢線
點電荷的電場域和等勢線對非點電荷間的相互作用力,可看成許多點電荷間相互作用力的疊加.靜止點電荷對運動點電荷的作用力可用庫侖定律計算,但運動點電荷對運動點電荷的作用力一般不能用庫侖定律計算 。
兩靜止點電荷間的相互作用是通過靜電場產生的。
在國際單位制里,電荷量的符號用Q表示,單位是庫倫(C)。
電場
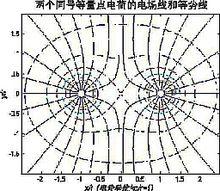 兩個同號等量點電荷的電場線和等勢線
兩個同號等量點電荷的電場線和等勢線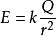 點電荷
點電荷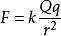 點電荷
點電荷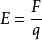 點電荷
點電荷點電荷的場強公式 ,是由庫侖定律 和場強的定義式 共同產生的,與庫侖定律一樣,具有以下一些特徵:① 必須是真空;② 必須是點電荷; ③ 都是平方反比關係,近一點則很強,遠一點則很弱。點電荷的電場線是用來形象地描述點電荷的電場的,正點電荷的電場線是一簇發散的直線,負點電荷的電場線是一簇收斂的直線。不論哪一種點電荷的電場線都是“近密遠疏”。這和點電荷的場強公式是一致的。
電勢與電勢能
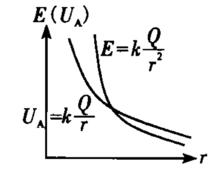 點電荷電勢與場強變化
點電荷電勢與場強變化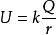 點電荷
點電荷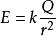 點電荷
點電荷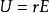 點電荷
點電荷點電荷的電勢可以簡單地看做是由和推導得到。很顯然,它與電場公式相比,形式相似,只是場強是平方反比關係,電勢是反比關係。從曲線上講,場強變化劇烈,電勢變化緩慢,常取無窮遠處電勢為零。
點電荷的等勢面是一簇“近密遠疏”的同心球殼,這一規律與其電場線的規律也是相似的。同時也體現了場強大處電勢差大,即“場強大處電壓高”的特點。
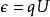 點電荷
點電荷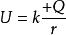 點電荷
點電荷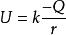 點電荷
點電荷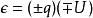 點電荷
點電荷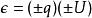 點電荷
點電荷點電荷的電勢能,由於正點電荷形成的電場中,各點的電勢均為正,負點電荷形成的電場中,各點的電勢均為負,所以引力勢能均為負,斥力勢能均為正。