概念
核外電子排布遵循泡利不相容原理、能量最低原理和洪特規則。能量最低原理就是在不違背泡利不相容原理的前提下,核外電子總是儘先占有能量最低的軌道,只有當能量最低的軌道占滿後,電子才依次進入能量較高的軌道,也就是儘可能使體系能量最低。洪特規則是在等價軌道(相同電子層、電子亞層上的各個軌道)上排布的電子將儘可能分占不同的軌道,且自旋方向相同。後來量子力學證明,電子這樣排布可使能量最低,所以洪特規則可以包括在能量最低原理中,作為能量最低原理的一個補充。
自旋為半整數的粒子(費米子)所遵從的一條原理。簡稱泡利原理。它可表述為全體費米子體系中不可能有兩個或兩個以上的粒子同時處於相同的單粒子態。電子的自旋,電子遵從泡利原理。根據泡利原理可很好地說明化學元素的周期律。泡利原理是全體費米子遵從的一條重要原則,在所有含有電子的系統中,在分子的化學價鍵理論中、在固態金屬、半導體和絕緣體的理論中都起著重要作用。後來知道泡利原理也適用於其他如質子、中子等費米子。泡利原理是認識許多自然現象的基礎。
最初泡利是在總結原子構造時提出一個原子中沒有任何兩個電子可以擁有完全相同的量子態。一個由2個費米子組成的量子系統波函式完全反對稱。
原理解釋
 泡利不相容原理
泡利不相容原理假如將任何兩個粒子對調後波函式的值的符號改變的話,那么這個波函式就是 完全反對稱的。這說明兩個費米子在同一個系統中永遠無法占據同一量子態。由於所有的量子粒子是不可區分的,假如兩個費米子的量子態完全相同的話,那么在將它們對換後波函式的值不應該改變。這個悖論的唯一解是該波函式的值為零:
比如在上面的例子中假如兩個粒子的位置波函式一致的話,那么它們的自旋波函式必須是反對稱的,也就是說它們的自旋必須是相反的。
該原理說明,兩個電子或者兩個任何其他種類的費米子,都不可能占據完全相同的量子態。通常也稱為泡利不相容原理(因奧地利物理學家泡利(1900~1958)而得名)。
原理的套用
泡利不相容原理是近代物理中一個基本的原理,由此可以導出很多的結果,這兒我們列舉該原理在近代物理中三個重要的套用,即確定同科電子原子態, 氦原子能級之謎和費米–狄拉克統計。
同科電子原子態
原子中電子的狀態用四個量子數(n, l, m, m)描述,其中n為主量子數,l為軌道角動量量子數,ml軌道磁量子數,ms為自旋磁量子數。使用四個量子數是現代通用的標記方法,而非泡利當時採用的標記。主量子數n和軌道角動量量子數 l 的電子稱為同科電子,同科電子的原子態需要考慮到泡利不相容原理的限制。泡利不相容原理表述為在原子中不可能有兩個或兩個以上電子具有完全相同的四個量子數(n, l, m,m)。
氦原子能級之謎
藉助於泡利不相容原理,海森堡提出了多電子原子的波函式具有反對稱性,最早揭開了氦原子能級之謎。
費米–狄拉克統計
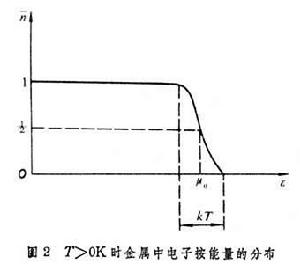
1926 年費米(E. Fermi)發現了遵循泡利不相容原理的單原子理想氣體所遵循的被稱為費米–狄拉克分布的 對稱波函式與其他勢能項相1926 年費米(E. Fermi)的函式,但費米沒有給出具體的導出過程。費米依據費米–狄拉克分布函式研究低溫下單原子理想氣體量子化(簡併)問題,費米給出了理想氣體的平均動能,壓強,熵和比熱的表示式(與溫度成正比),解決了金屬中自由電子對比熱貢獻的難題。
同年狄拉克一篇研究量子力學理論的文章中構造出滿足泡利不相容理論的多粒子體系的反對稱波函式 ,狄拉克還意識到滿足玻色–愛因斯坦統計的波函式是多粒子波函式是對稱的。狄拉克還獨立地導出了滿足泡利不相容原理的全同粒子在不同能級不同溫度下的費米–狄拉克分布函式,依據費米–狄拉克分布函式還研究了費米氣體的能量,壓強並且指出了費米氣體比熱正比於溫度一次方,還發展了微擾論給出了愛因斯坦受激輻射理論中B係數的表達式。這兒我們跟隨狄拉克從泡利不相容原理出發導出費米–狄拉克分布函式。