高斯濾波概述
簡介實質上是一種信號的濾波器,其用途是信號的平滑處理,我們知道數字圖像用於後期套用,其噪聲是最大的問題,由於誤差會累計傳遞等原因,很多圖像處理教材會在很早的時候介紹Gauss濾波器,用於得到信噪比SNR較高的圖像(反應真實信號)。於此相關的有Gauss-Laplace變換,其實就是為了得到較好的圖像邊緣,先對圖像做Gauss平滑濾波,剔除噪聲,然後求二階導矢,用二階導的過零點確定邊緣,在計算時也是頻域乘積=>空域卷積。
模型濾波器就是建立的一個數學模型,通過這個模型來將圖像數據進行能量轉化,能量低的就排除掉,噪聲就是屬於低能量部分
摘要
高斯濾波實質上是一種信號的濾波器,其用途是信號的平滑處理,我們知道數字圖像用於後期套用,其噪聲是最大的問題,由於誤差會累計傳遞等原因,很多圖像處理教材會在很早的時候介紹Gauss濾波器,用於得到信噪比SNR較高的圖像(反應真實信號)。與此相關的有Gauss-Lapplace變換,其實就是為了得到較好的圖像邊緣,先對圖像做Gauss平滑濾波,剔除噪聲,然後求二階導矢,用二階導的過零點確定邊緣,在計算時也是頻域乘積=>空域卷積。
濾波器就是建立的一個數學模型,通過這個模型來將圖像數據進行能量轉化,能量低的就排除掉,噪聲就是屬於低能量部分
其實編程運算的話就是一個模板運算,拿圖像的八連通區域來說,中間點的像素值就等於八連通區的像素值的均值,這樣達到平滑的效果。
若使用理想濾波器,會在圖像中產生振鈴現象。採用高斯濾波器的話,系統函式是平滑的,避免了振鈴現象。
原理及套用
原理其實編程運算的話就是一個模板運算,拿圖像的八連通區域來說,中間點的像素值就等於八連通區的像素值的均值,這樣達到平滑的效果
若使用理想濾波器,會在圖像中產生振鈴現象。採用高斯濾波器的話,系統函式是平滑的,避免了振鈴現象。
由於高斯函式的傅立葉變換仍是高斯函式, 因此高斯函式能構成一個在頻域具有平滑性能的低通濾波器。可以通過在頻域做乘積來實現高斯濾波。均值濾波是對信號進行局部平均, 以平均值來代表該像素點的灰度值。矩形濾波器(Averaging Box Filter)對這個二維矢量的每一個分量進行獨立的平滑處理。通過計算和轉化 ,得到一幅單位矢量圖。這個 512×512的矢量圖被劃分成一個 8×8的小區域 ,再在每一個小區域中 ,統計這個區域內的主要方向 ,亦即將對該區域內點方向數進行統計,最多的方向作為區域的主方向。於是就得到了一個新的64×64的矢量圖。這個新的矢量圖還可以採用一個 3×3模板進行進一步的平滑。
高斯濾波器是一類根據高斯函式的形狀來選擇權值的線性平滑濾波器。它對去除服從常態分配的噪聲很有效。
常用的零均值離散高斯濾波器函式: g(x)=exp( -x^2/(2 sigma^2)
其中,高斯分布參數Sigma決定了高斯函式的寬度。對於圖像處理來說,常用二維零均值離散高斯函式作平滑濾波器。
高斯函式具有五個重要的性質,這些性質使得它在早期圖像處理中特別有用.這些性質表明,高斯平滑濾波器無論在空間域還是在頻率域都是十分有效的低通濾波器,且在實際圖像處理中得到了工程人員的有效使用.高斯函式具有五個十分重要的性質,它們是:
(1)二維高斯函式具有鏇轉對稱性,即濾波器在各個方向上的平滑程度是相同的.一般來說,一幅圖像的邊緣方向是事先不知道的,因此,在濾波前是無法確定一個方向上比另一方向上需要更多的平滑.鏇轉對稱性意味著高斯平滑濾波器在後續邊緣檢測中不會偏向任一方向.
(2)高斯函式是單值函式.這表明,高斯濾波器用像素鄰域的加權均值來代替該點的像素值,而每一鄰域像素點權值是隨該點與中心點的距離單調增減的.這一性質是很重要的,因為邊緣是一種圖像局部特徵,如果平滑運算對離運算元中心很遠的像素點仍然有很大作用,則平滑運算會使圖像失真.
(3)高斯函式的付立葉變換頻譜是單瓣的.正如下面所示,這一性質是高斯函式付立葉變換等於高斯函式本身這一事實的直接推論.圖像常被不希望的高頻信號所污染(噪聲和細紋理).而所希望的圖像特徵(如邊緣),既含有低頻分量,又含有高頻分量.高斯函式付立葉變換的單瓣意味著平滑圖像不會被不需要的高頻信號所污染,同時保留了大部分所需信號.
(4)高斯濾波器寬度(決定著平滑程度)是由參數σ表征的,而且σ和平滑程度的關係是非常簡單的.σ越大,高斯濾波器的頻帶就越寬,平滑程度就越好.通過調節平滑程度參數σ,可在圖像特徵過分模糊(過平滑)與平滑圖像中由於噪聲和細紋理所引起的過多的不希望突變數(欠平滑)之間取得折衷.
(5)由於高斯函式的可分離性,較大尺寸的高斯濾波器可以得以有效地實現.二維高斯函式卷積可以分兩步來進行,首先將圖像與一維高斯函式進行卷積,然後將卷積結果與方向垂直的相同一維高斯函式卷積.因此,二維高斯濾波的計算量隨濾波模板寬度成線性增長而不是成平方增長.
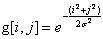 高斯函式
高斯函式