基本介紹
高斯模糊(Gaussian Blur)是美國Adobe圖像軟體公司開發的一個圖像處理軟體:Adobe Photoshop(系列)中的一個濾鏡,具體的位置在:濾鏡—模糊——高斯模糊!高斯模糊的原理中,它是根據高斯曲線調節象素色值,它是有選擇地模糊圖像。說得直白一點,就是高斯模糊能夠把某一點周圍的像素色值按高斯曲線統計起來,採用數學上加權平均的計算方法得到這條曲線的色值,最後能夠留下人物的輪廓,即曲線.是指當 Adobe Photoshop 將加權平均套用於像素時生成的鐘形曲線。
在PS中間,你應該知道所有的顏色不過都是數字,各種模糊不過都是算法。把要模糊的像素色值統計,用數學上加權平均的計算方法(高斯函式)得到色值,對範圍、半徑等進行模糊,大致就是高斯模糊。
原理
周邊像素的平均值
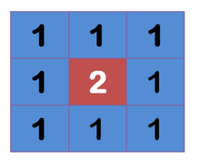 高斯模糊原理的圖解
高斯模糊原理的圖解所謂"模糊",可以理解成每一個像素都取周邊像素的平均值。
右圖中,2是中間點,周邊點都是1。
"中間點"取"周圍點"的平均值,就會變成1。在數值上,這是一種"平滑化"。在圖形上,就相當於產生"模糊"效果,"中間點"失去細節。
顯然,計算平均值時,取值範圍越大,"模糊效果"越強烈。
 高斯模糊
高斯模糊左圖分別是原圖、模糊半徑3像素、模糊半徑10像素的效果。模糊半徑越大,圖像就越模糊。從數值角度看,就是數值越平滑。
接下來的問題就是,既然每個點都要取周邊像素的平均值,那么應該如何分配權重呢?
如果使用簡單平均,顯然不是很合理,因為圖像都是連續的,越靠近的點關係越密切,越遠離的點關係越疏遠。因此,加權平均更合理,距離越近的點權重越大,距離越遠的點權重越小。
常態分配的權重
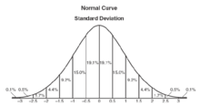 高斯模糊
高斯模糊常態分配顯然是一種可取的權重分配模式。
在圖形上,常態分配是一種鐘形曲線,越接近中心,取值越大,越遠離中心,取值越小。
計算平均值的時候,我們只需要將"中心點"作為原點,其他點按照其在正態曲線上的位置,分配權重,就可以得到一個加權平均值。
高斯函式
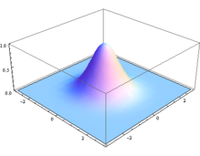 高斯模糊
高斯模糊上面的常態分配是一維的,圖像都是二維的,所以我們需要二維的常態分配。
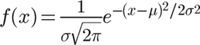 一維形式
一維形式常態分配的密度函式叫做"高斯函式"(Gaussian function)。它的一維形式是:
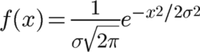 進一步推導
進一步推導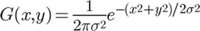 二維高斯函式
二維高斯函式其中,μ是x的均值,σ是x的方差。因為計算平均值的時候,中心點就是原點,所以μ等於0。根據一維高斯函式,可以推導得到二維高斯函式:
有了這個函式 ,就可以計算每個點的權重了。
權重矩陣
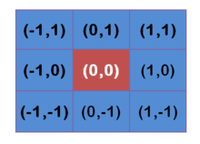 權重矩陣
權重矩陣假定中心點的坐標是(0,0),那么距離它最近的8個點的坐標如下:
更遠的點以此類推。
為了計算權重矩陣,需要設定σ的值。假定σ=1.5,則模糊半徑為1的權重矩陣如下:
這9個點的權重總和等於0.4787147,如果只計算這9個點的加權平均,還必須讓它們的權重之和等於1,因此上面9個值還要分別除以0.4787147,得到最終的權重矩陣。
計算高斯模糊
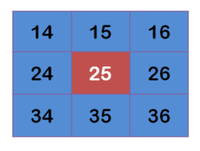 計算高斯模糊
計算高斯模糊有了權重矩陣,就可以計算高斯模糊的值了。假設現有9個像素點,灰度值(0-255)如下:
每個點乘以自己的權重值:
得到
將這9個值加起來,就是中心點的高斯模糊的值。
對所有點重複這個過程,就得到了高斯模糊後的圖像。如果原圖是彩色圖片,可以對RGB三個通道分別做高斯模糊。
高斯模糊矩陣示例表
這是一個計算 σ = 0.84089642 的高斯分布生成的示例矩陣。注意中心元素 [4,4]] 處有最大值,隨著距離中心越遠數值對稱地減小。
| 0.00000067 | 0.00002292 | 0.00019117 | 0.00038771 | 0.00019117 | 0.00002292 | 0.00000067 |
| 0.00002292 | 0.00078633 | 0.00655965 | 0.01330373 | 0.00655965 | 0.00078633 | 0.00002292 |
| 0.00019117 | 0.00655965 | 0.05472157 | 0.11098164 | 0.05472157 | 0.00655965 | 0.00019117 |
| 0.00038771 | 0.01330373 | 0.11098164 | 0.22508352 | 0.11098164 | 0.01330373 | 0.00038771 |
| 0.00019117 | 0.00655965 | 0.05472157 | 0.11098164 | 0.05472157 | 0.00655965 | 0.00019117 |
| 0.00002292 | 0.00078633 | 0.00655965 | 0.01330373 | 0.00655965 | 0.00078633 | 0.00002292 |
| 0.00000067 | 0.00002292 | 0.00019117 | 0.00038771 | 0.00019117 | 0.00002292 | 0.00000067 |
注意中心處的 0.22508352 比 3σ 外的 0.00019117 大 1177 倍。
Java程式實現
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 | import java.awt.Color; import java.awt.image.BufferedImage; import java.io.File; import java.io.IOException; import javax.imageio.ImageIO; public class Test { /** * 簡單高斯模糊算法 * * @param args * @throws IOException [參數說明] * * @return void [返回類型說明] * @exception throws [ 違例 類型] [違例說明] * @see [類、類#方法、類#成員] */ public static void main (String[] args) throws IOException { BufferedImage img = ImageIO.read(new File("d:\\My Documents\\psb.jpg")); System.out.println(img); int height = img.getHeight(); int width = img.getWidth(); int[][] matrix = new int[3][3]; int[] values = new int[9]; for (int i = 0; i < width; i++) { for (int j = 0; j < height; j++ ) { readPixel(img, i, j, values); fillMatrix(matrix, values); img.setRGB(i, j, avgMatrix(matrix)); } } ImageIO.write(img, "jpeg", new File("d:/test.jpg"));//保存在d盤為test.jpeg檔案 } private static void readPixel(BufferedImage img, int x, int y, int[] pixels) { int xStart = x - 1; int yStart = y - 1; int current = 0; for (int i = xStart; i < 3 + xStart; i++) { for (int j = yStart; j < 3 + yStart; j++) { int tx = i; if (tx < 0) { tx = -tx; } else if (tx >= img.getWidth()) { tx = x; } int ty = j; if (ty < 0) { ty = -ty; } else if (ty >= img.getHeight()) { ty = y; } pixels[current++] = img.getRGB(tx, ty); } } } private static void fillMatrix(int[][] matrix, int... values) { int filled = 0; for (int i = 0; i < matrix.length; i++) { int[] x = matrix[i]; for (int j = 0; j < x.length; j++) { x[j] = values[filled++]; } } } private static int avgMatrix(int[][] matrix) { int r = 0; int g = 0; int b = 0; for (int i = 0; i < matrix.length; i++) { int[] x = matrix[i]; for (int j = 0; j < x.length; j++) { if (j == 1) { continue; } Color c = new Color(x[j]); r += c.getRed(); g += c.getGreen(); b += c.getBlue(); } } return new Color(r / 8, g / 8, b / 8).getRGB(); } } |

