馬蒂厄方程
馬蒂厄在研究橢圓形膜的邊界值問題時,導出了一個二階常微分方程,其形式為
 馬蒂厄函式
馬蒂厄函式 馬蒂厄函式
馬蒂厄函式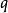 馬蒂厄函式
馬蒂厄函式 馬蒂厄函式
馬蒂厄函式 馬蒂厄函式
馬蒂厄函式式中, 和 為二個實參數,方程的係數是以 或 為周期的。
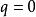 馬蒂厄函式
馬蒂厄函式當 時,馬蒂厄方程退化為
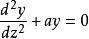 馬蒂厄函式
馬蒂厄函式 馬蒂厄函式
馬蒂厄函式解為
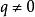 馬蒂厄函式
馬蒂厄函式當 時,可以得到分情況分別得到整數階的馬蒂厄函式和非整數階的馬蒂厄函式
整數階的馬蒂厄函式
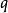 馬蒂厄函式
馬蒂厄函式 馬蒂厄函式
馬蒂厄函式在很多實際問題中,馬蒂厄方程所描寫的系統稱為參量激勵型的, 代表激勵幅度的大小,當這種激勵並不十分強烈時,可以將它作為數學處理中的微擾參數,若 不能表示為某個整數的平方但可以表示為
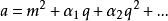 馬蒂厄函式
馬蒂厄函式 馬蒂厄函式
馬蒂厄函式 馬蒂厄函式
馬蒂厄函式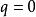 馬蒂厄函式
馬蒂厄函式當 時,有 ,這時,可以認為馬蒂厄方程的解偏離 時的馬蒂厄方程的解組並不太大,於是對應於餘弦項的解組可表示為
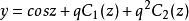 馬蒂厄函式
馬蒂厄函式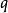 馬蒂厄函式
馬蒂厄函式 馬蒂厄函式
馬蒂厄函式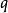 馬蒂厄函式
馬蒂厄函式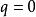 馬蒂厄函式
馬蒂厄函式將該式代入馬蒂厄方程,將所得的結果按照 的冪次排列,使得各個冪次前的係數相等,於是可以得到待定係數 的值,將這些值帶入上式中,我們可以得到一階橢圓餘弦函式或者稱為餘弦型一階馬蒂厄函式,類似的,我們可以得到對應正弦項的解稱為一階橢圓正弦函式或者正弦型一階馬蒂厄函式。當 一定時,這兩個解的特徵數不相等,這表明這兩個馬蒂厄函式不能同時成為馬蒂厄方程的解,除非 。
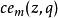 馬蒂厄函式
馬蒂厄函式但是馬蒂厄方程應該有兩個線性獨立的解,這就求助於構造獨立解的方法。例如,已知一個解為 ,與它線性獨立的另一個解可以用它們的朗斯基行列式求得,即
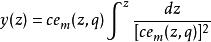 馬蒂厄函式
馬蒂厄函式 馬蒂厄函式
馬蒂厄函式同理,我們可以得到 階的馬蒂厄函式。
非整數階的馬蒂厄函式
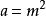 馬蒂厄函式
馬蒂厄函式 馬蒂厄函式
馬蒂厄函式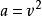 馬蒂厄函式
馬蒂厄函式 馬蒂厄函式
馬蒂厄函式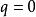 馬蒂厄函式
馬蒂厄函式 馬蒂厄函式
馬蒂厄函式 馬蒂厄函式
馬蒂厄函式上面我們討論了 ,其中, 為整數的情形,現在我們來研究 , 為非整數時的情況。與上面的計算方法類似,當 時,退化的馬蒂厄方程的解組為 和 。
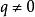 馬蒂厄函式
馬蒂厄函式當 ,兩個解組可以表示為
 馬蒂厄函式
馬蒂厄函式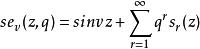 馬蒂厄函式
馬蒂厄函式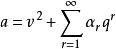 馬蒂厄函式
馬蒂厄函式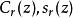 馬蒂厄函式
馬蒂厄函式 馬蒂厄函式
馬蒂厄函式將這些結果分別代入馬蒂厄方程分別定出 及對應的 的值,將這些值代入上式得到兩個解組的值,這兩個解組的特徵數相同,於是這兩個解組是可以共存的,故可作為二個線性獨立解,使得馬蒂厄方程的任何一個解可以由它們的線性組合表示。
連帶馬蒂厄函式
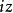 馬蒂厄函式
馬蒂厄函式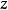 馬蒂厄函式
馬蒂厄函式如果在馬蒂厄方程中用 置換 ,則得到下面的微分方程:
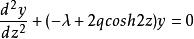 馬蒂厄函式
馬蒂厄函式該方程的解
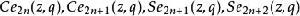 馬蒂厄函式
馬蒂厄函式稱為連帶馬蒂厄函式。
