簡介
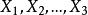 馬爾可夫模型狀態
馬爾可夫模型狀態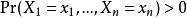 馬爾可夫模型狀態
馬爾可夫模型狀態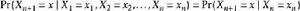 馬爾可夫模型狀態
馬爾可夫模型狀態馬爾可夫模型狀態是指馬爾可夫性質的隨機變數序列 的當前狀態,過去狀態和未來狀態。給定當前狀態,將來狀態和過去狀態是相互獨立的。t+1 時刻系統狀態的機率分布只與t 時刻的狀態有關與t時刻以前的狀態無關;從t時刻到t+1 時刻的狀態轉移與t的值無關。一個馬爾可夫鏈模型可表示為=(S,P, Q),其中各字母的含義如下:S 是系統所有可能的狀態所組成的非空的狀態集,有時也稱之為系統的狀態空間,它可以是有限的、可列的集合或任意非空集。狀態之間關係滿足馬爾可夫性質,不同狀態之間轉移有一個確定的機率分布,通常用一系列有向圖來來描述狀態之間的關係。馬爾可夫性質(Markov property)是機率論中的一個概念,因為俄國數學家安德雷·馬爾可夫得名。當一個隨機過程在給定當前狀態及所有過去狀態情況下,其未來狀態的條件機率分布僅依賴於當前狀態;換句話說,在給定當前狀態時,它與過去狀態(即該過程的歷史路徑)是條件獨立的,那么此隨機過程即具有馬爾可夫性質。具有馬爾可夫性質的過程通常稱之為馬爾可夫過程。從形式上看,如果兩邊的條件分布有定義(即如果 ),則 .X的可能值構成的可數集S叫做該鏈的“狀態空間”。
瞬態演變
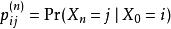 馬爾可夫模型狀態
馬爾可夫模型狀態用n步從狀態i到狀態j的機率為 ,
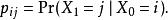 馬爾可夫模型狀態
馬爾可夫模型狀態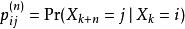 馬爾可夫模型狀態
馬爾可夫模型狀態而單步轉移是 ,對於一個時齊馬爾可夫鏈來說: ,
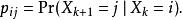 馬爾可夫模型狀態
馬爾可夫模型狀態而且
n步轉移機率滿足Chapman-Kolmogorov等式,對任意k使得0 < k < n,
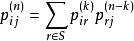 馬爾可夫模型狀態
馬爾可夫模型狀態其中S為此馬爾可夫鏈的狀態空間。
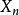 馬爾可夫模型狀態
馬爾可夫模型狀態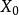 馬爾可夫模型狀態
馬爾可夫模型狀態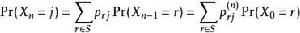 馬爾可夫模型狀態
馬爾可夫模型狀態邊緣分布Pr( = x)為第n次狀態的分布。初始分布為Pr( = x)。用一步轉移把過程演變描述為
馬爾可夫模型
馬爾可夫模型是一種在給定當前信息的情況下,歷史狀態與未來狀態無關的隨機過程。若模型在t時刻的狀態只與t-1時刻的狀態有關,而與其他時刻狀態無關,則稱為一階馬爾可夫模型 。在馬爾可夫鏈的每一步,系統根據機率分布,可以從一個狀態變到另一個狀態,也可以保持當前狀態。狀態的改變叫做轉移,與不同的狀態改變相關的機率叫做轉移機率。隨機漫步就是馬爾可夫鏈的例子。隨機漫步中每一步的狀態是在圖形中的點,每一步可以移動到任何一個相鄰的點,在這裡移動到每一個點的機率都是相同的(無論之前漫步路徑是如何的)。隱馬爾可夫模型(Hidden Markov Model,HMM)是統計模型,它用來描述一個含有隱含未知參數的馬爾可夫過程。其難點是從可觀察的參數中確定該過程的隱含參數。然後利用這些參數來作進一步的分析,例如模式識別。在正常的馬爾可夫模型中,狀態對於觀察者來說是直接可見的。這樣狀態的轉換機率便是全部的參數。而在隱馬爾可夫模型中,狀態並不是直接可見的,但受狀態影響的某些變數則是可見的。每一個狀態在可能輸出的符號上都有一機率分布。因此輸出符號的序列能夠透露出狀態序列的一些信息。
隱馬爾可夫模型(Hidden Markov Model,HMM)是統計模型,它用來描述一個含有隱含未知參數的馬爾可夫過程。其難點是從可觀察的參數中確定該過程的隱含參數。然後利用這些參數來作進一步的分析,例如模式識別。在正常的馬爾可夫模型中,狀態對於觀察者來說是直接可見的。這樣狀態的轉換機率便是全部的參數。而在隱馬爾可夫模型中,狀態並不是直接可見的,但受狀態影響的某些變數則是可見的。每一個狀態在可能輸出的符號上都有一機率分布。因此輸出符號的序列能夠透露出狀態序列的一些信息。
有向圖
一類重要的圖。它是對每一條邊都規定一個方向的圖。確切地說,一個有向圖D,就是一個集合的二元組D=(V(D),A(D)),其中V(D)是一個非空的有限集,其元素稱為節點,A(D)是由V(D)的元素的一些有序對構成的集合。稱A(D)的元素為D的弧。與弧關聯的兩個節點也稱為它的端點,並規定弧的方向為從始端指向終端。在一個有向圖中,它的一個節點的出次就是離開這個節點的關聯邊的數目;入次就是指向這個節點的關聯邊的數目。一個節點的次就是它的出次與入次的和。若把一個有向圖的每一條弧代之以無向的連結相同端點的邊,則稱所得圖為該有向圖的基礎圖或母圖。若把一個有向圖的每一條弧代之以連結相同端點的相反方向的弧,則稱所得有向圖為原有向圖的逆向圖。若在一個有向圖上,每一條弧都有一條與它方向相反且端點相同的弧,則稱這個有向圖為對稱有向圖。若存在一個整數k,一個有向圖的鄰接矩陣的k次冪中的元素都為正數,則稱這個有向圖為本原有向圖。對於有向圖有一些與方向有關的對偶概念,如出次和入次、出樹和入樹等。若一個與方向有關的命題成立,將其中的概念換為其對偶概念,則所得命題也一定成立。這就是方向對偶原則。

