簡介
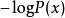香農-范諾編碼香農-范諾編碼其名稱來自於以克勞德·香農和羅伯特·法諾。在理想意義上，它與哈夫曼編碼一樣，並未實現碼詞（code word）長度的最低預期;然而，與哈夫曼編碼不同的是，它確保了所有的碼詞長度在一個理想的理論範圍 之內。這項技術是香農於1948年，在他介紹信息理論的文章“通信數學理論”中被提出的。這個方法歸功於范諾，他在不久以後以技術報告發布了它。香農-范諾編碼不應該與香農編碼混淆，後者的編碼方法用於證明Shannon's noiseless coding theorem，或與Shannon–Fano–Elias coding（又被稱作Elias coding）一起，被看做算術編碼的先驅 。
香農-范諾編碼，符號從最大可能到最少可能排序，將排列好的信源符號分化為兩大組，使兩組的機率和近於相同，並各賦予一個二元碼符號“0”和“1”。只要有符號剩餘，以同樣的過程重複這些集合以此確定這些代碼的連續編碼數字。依次下去，直至每一組的只剩下一個信源符號為止。當一組已經降低到一個符號，顯然，這意味著符號的代碼是完整的，不會形成任何其他符號的代碼前綴。
這是一個行之有效的算法，它會產生相當有效的可變長度編碼;當兩個較小的集生產分區其實是相等的機率，一位用於區分它們的信息是最有效的使用。不幸的是，香農 - 法諾並不總是產生最優的前綴碼：機率{0.35，0.17，0.17，0.16，0.15}是一個將分配非最佳化代碼的Shannon-Fano的編碼的一個例子。
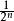香農-范諾編碼出於這個原因，香農 - 范諾幾乎從不使用; 哈夫曼編碼幾乎是計算簡單，生產總是達到預期最低的碼字長度的制約下，每個符號是由一個整數組成一個代碼代表的前綴碼。這往往是不必要的，因為代碼將裝在首尾相連的長序列的里。如果我們認為一次的代碼組，象徵符號的哈夫曼編碼是最佳符號的機率統計獨立|獨立和一些半功率，即，為 。在大多數情況下，算術編碼可以產生比哈夫曼或的香農-范諾更大的整體壓縮，因為它可以在小數位編碼，這更接近實際的符號信息內容。然而，算術編碼並沒有取代像霍夫曼取代的香農-范諾一樣取代哈夫曼，一方面是因為算術編碼的計算成本的方式，因為它是由多個專利覆蓋。香農：范諾編碼被用在爆聚壓縮方法。
香農-范諾算法
Shannon-Fano的樹是根據旨在定義一個有效的代碼表的規範而建立的。實際的算法很簡單：
對於一個給定的符號列表，制定了機率相應的列表或頻率計數，使每個符號的相對發生頻率是已知。
排序根據頻率的符號列表，最常出現的符號在左邊，最少出現的符號在右邊。
清單分為兩部分，使左邊部分的總頻率和儘可能接近右邊部分的總頻率和。
該列表的左半邊分配二進制數字0，右半邊是分配的數字1。這意味著，在第一半符號代都是將所有從0開始，第二半的代碼都從1開始。
對左、右半部分遞歸套用步驟3和4，細分群體，並添加位的代碼，直到每個符號已成為一個相應的代碼樹的葉。
1.對於一個給定的符號列表，制定了機率相應的列表或頻率計數，使每個符號的相對發生頻率是已知。
2.排序根據頻率的符號列表，最常出現的符號在左邊，最少出現的符號在右邊。
3.清單分為兩部分，使左邊部分的總頻率和儘可能接近右邊部分的總頻率和。
4.該列表的左半邊分配二進制數字0，右半邊是分配的數字1。這意味著，在第一半符號代都是將所有從0開始，第二半的代碼都從1開始。
5.對左、右半部分遞歸套用步驟3和4，細分群體，並添加位的代碼，直到每個符號已成為一個相應的代碼樹的葉。
示例
這個例子展示了一組字母的香農編碼結構（如圖a所示）這五個可被編碼的字母有如下出現次數：
| 符號 | A | B | C | D | E |
| 計數 | 15 | 7 | 6 | 6 | 5 |
| 機率 | 0.38461538 | 0.17948718 | 0.15384615 | 0.15384615 | 0.12820513 |
從左到右，所有的符號以它們出現的次數劃分。在字母B與C之間劃定分割線，得到了左右兩組，總次數分別為22,17。這樣就把兩組的差別降到最小。通過這樣的分割, A與B同時擁有了一個以0為開頭的碼字, C，D，E的碼子則為1,如圖b所示。隨後，在樹的左半邊，於A，B間建立新的分割線，這樣A就成為了碼字為00的葉子節點，B的碼子01。經過四次分割，得到了一個樹形編碼。如下表所示，在最終得到的樹中，擁有最大頻率的符號被兩位編碼，其他兩個頻率較低的符號被三位編碼。
| 符號 | A | B | C | D | E |
| 編碼 | 00 | 01 | 10 | 110 | 111 |
根據A，B，C兩位編碼長度，D，E的三位編碼長度，最終的平均碼字長度是
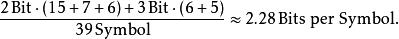香農-范諾編碼
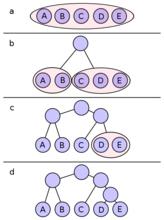香農-范諾編碼算法