顏色矩

顏色是彩色圖像最重要的內容之一，被廣泛用於圖像檢索中。但從圖像中提取顏色特徵時，很多算法都先要對圖像進行量化處理。量化處理容易導致誤檢，並且產生的圖像特徵維數較高，不利於檢索。

AMA Stricker和M Orengo提出了顏色矩的方法 ，顏色矩是一種簡單有效的顏色特徵表示方法，有一階矩(均值,mean)、二階矩(方差, variance)和三階矩(斜度,skewness)等，由於顏色信息主要分布於低階矩中，所以用一階矩，二階矩和三階矩足以表達圖像的顏色分布，顏色矩已證明可有效地表示圖像中的顏色分布，該方法的優點在於：不需要顏色空間量化，特徵向量維數低；但實驗發現該方法的檢索效率比較低，因而在實際套用中往往用來過濾圖像以縮小檢索範圍。

三個顏色矩的數學定義如下：

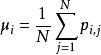顏色矩

顏色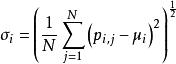矩

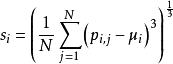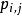顏色矩

顏色矩

其中， 表示彩色圖像第j個像素的第i個顏色分量，N表示圖像中的像素個數。

圖像的三個分量Y,U,V圖像的前三階顏色矩組成一個9維直方圖向量，即圖像的顏色特徵表示如下：

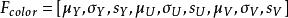顏色矩