定義
頻域是描述信號在頻率方面特性時用到的一種坐標系。在電子學,控制系統工程和統計學中,頻域圖顯示了在一個頻率範圍內每個給定頻帶內的信號量 。
幅度和相位
在使用拉普拉斯,Z-或傅立葉變換時,信號由頻率的複函數描述:在任何給定頻率的信號的分量由複數給出。數字的幅度是該分量的幅度,角度是波的相對相位。
 頻譜分析儀
頻譜分析儀例如,使用傅立葉變換,諸如人類語音的聲波可以被分解成其不同頻率的音調分量,每個音調分量由具有不同幅度和相位的正弦波表示。系統的回響作為頻率的函式,也可以通過複函數來描述。在許多套用中,相位信息並不重要。通過丟棄相位信息,可以簡化頻域表示中的信息以生成頻譜或頻譜密度。頻譜分析儀是顯示頻譜的設備,而時域頻率可以在示波器上看到。
功率譜密度是可以套用於既不是周期性的也不是可平方積分的大類信號的頻域描述;具有功率譜密度,信號僅需要是廣義靜態隨機過程的輸出。
不同的頻域
頻域分析時域函式的多個不同的數學變換被稱為“頻域”方法。 這些是最常見的變換及其套用:
傅立葉級數 - 重複信號,振盪系統
傅立葉變換 - 非重現信號,瞬變
拉普拉斯變換 - 電子電路和控制系統
Z變換 - 離散信號,數位訊號處理
小波變換 - 圖像分析,數據壓縮
上述變換可以被解釋為捕獲某種形式的頻率,因此變換域被稱為頻域。
離散頻域
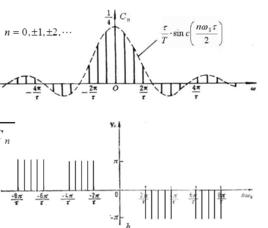
周期信號的傅立葉變換僅具有在基頻及其諧波的能量。 也就是,可以使用離散頻域來分析周期信號。 反過來,離散時間信號產生周期性頻譜。 結合這兩個特點,如果我們從一個離散和周期性的時間信號開始,就可以得到一個周期性和離散性的頻譜。
頻域分析
頻域(頻率域)——自變數是頻率,即橫軸是頻率,縱軸是該頻率信號的幅度,也就是通常說的頻譜圖。頻譜圖描述了信號的頻率結構及頻率與該頻率信號幅度的關係。
對信號進行時域分析時,有時一些信號的時域參數相同,但並不能說明信號就完全相同。因為信號不僅隨時間變化,還與頻率、相位等信息有關,這就需要進一步分析信號的頻率結構,並在頻率域中對信號進行描述。動態信號從時間域變換到頻率域主要通過傅立葉級數和傅立葉變換。
Bode圖
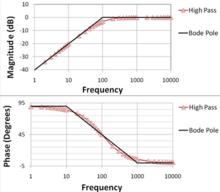 Bode圖
Bode圖在電氣工程和控制理論中,波德圖/boʊdi/是系統的頻率回響的曲線圖。 它通常是表示頻率回響的幅度(通常以分貝為單位)的Bode幅度圖和表示相移的Bode相點陣圖的組合。 兩個量都針對與頻率的對數成比例的水平軸繪製。假定分貝本身是對數標度,波德幅度圖是對數對數圖,而波德相點陣圖是線性對數圖。
傅立葉定理
在過程對象的Bode圖中表現出來的增益係數和相位滯後值,反映了系統的非常確定的特徵。由此,控制工程師運用此工具,不僅可以預測“系統未來對於正弦波的控制作用所產生的系統回響”,而且能夠知道“系統對任何控制作用所產生的系統回響”。
傅立葉定理
傅立葉定理使得以上的分析成為可能,該定理表明任何連續測量的時序或信號,都可以表示為不同頻率的正弦波信號的無限疊加。數學家傅立葉在1822年證明了這個著名的定理,並創造了為大家熟知的、被稱之為傅立葉變換的算法,該算法利用直接測量到的原始信號,以累加方式來計算不同正弦波信號的頻率、振幅和相位。
預測作用
從理論上說,傅立葉變換和Bode圖可以結合在一起使用,用以預測當線性過程對象受到控制作用的時序影響時產生的反應。詳見以下:
1) 利用傅立葉變換這一數學方法,把提供給過程對象的控制作用,從理論上分解為不同的正弦波的信號組成或者頻譜。
2) 利用Bode圖可以判斷出,每種正弦波信號在經由過程對象時發生了那些變化。換言之,在該圖上可以找到正弦波在每種頻率下的振幅和相位的改變。
3) 反之,利用反傅立葉變換這一方法,又可以將每個單獨改變的正弦波信號轉換成一個信號。
時間-頻率分析
在信號處理中,時間 - 頻率分析包括使用各種時間 - 頻率表示同時研究時域和頻域中的信號的那些技術。 不是觀察一維信號(一個函式,實數或復值)和一些變換(另一個函式,通過一些變換從原始數據中獲得),時頻分析研究二維信號 - 其域是二維實平面的函式,其通過時間 - 頻率變換從信號獲得。
信號頻域分析
概念
是採用傅立葉變換將時域信號x(t)變換為頻域信號X(f)的方法,幫助人們從另一個角度來了解信號的特徵。信號頻譜代表了信號在不同頻率分量成分的大小,能夠提供比時域信號波形更直觀,豐富的信息.
信號頻域分析是以輸入信號的頻率為變數,在頻率域,研究系統的結構參數與性能的關係,揭示了信號內在的頻率特性以及信號時間特性與其頻率特性之間的密切關係,從而導出了信號的頻譜、頻寬以及濾波、調製和頻分復用等重要概念。
優點
1、無需求解微分方程,圖解(頻率特性圖)法,間接揭示系統性能並指明改進性能的方向和易於實驗分析.
2、可推廣套用於某些非線性系統(如含有延遲環節的系統)以及可方便設計出能有效抑制噪聲的系統。
要素
分析系統的
⒈頻率回響,它指系統對正弦輸入信號的穩態回響。
⒉頻率特性,它指系統在不同頻率的正弦信號輸入時,其穩態輸出隨頻率而變化(ω由0變到∞)的特性。
⒊幅頻特性與相頻特性一起構成系統的頻率特性。
⒋幅頻特性,它指的是當ω由0到∞變化時,|G(jω)|的變化特性,記為A(ω)。
⒌相頻特性,它指的是當ω由0到∞變化時,∠G(jω)的變化特性稱為相頻特性,記為ϕ(ω)。