所謂預測，就是利用已知信號的樣值對未知信號樣值進行的估計。不失一般性，假定信號在當前時刻的值為 X，並且其前面 N個時刻的值分別為 X,…， X，如果用他們對 X進行預測，並用表示預測值，用{ a| i=1，…， N}表示預測係數，則預測公式可以寫成：
預測原理(1.1)
預測效果的好壞與預測係數的選擇有關，通常採用均方誤差極小準則選擇預測係數，在此條件下，預測係數應該滿足以下關係：
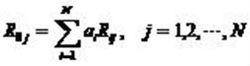預測原理(1.2)
這是一個 N階線性方程組，其中， R=E[X X]是信號的協方差，由此可解出 N個預測係數{ a| i=1,…， N}。由於它們使預測誤差的均方值極小，稱之為最佳預測係數。
在最佳預測的前提下，預測誤差的均方值為：
(1.3)
預測原理
預測原理為信號的方差。由此可見，，這說明誤差序列的方差比信號序列的方差要小，甚至可能小很多。另一方面，其相關性也比原始信號序列的相關性弱一些，甚至弱很多。誤差信號分布的一個最簡單的例子就是圖像差值信號的分布。當採用高階的最佳預測時，誤差信號的分布就會更加尖銳。預測誤差信號的這種不均勻分布的特點是進行DPCM壓縮編碼的重要依據。
在對預測誤差信號進行編碼時，有以下兩種不同的考慮：
（1）無失真預測編碼
直接對預測誤差進行熵編碼。在某些場合，希望經過編碼後能夠精確恢復原始信息，例如對一些航天探測器發回的圖片編碼等，就不希望採用任何不可逆的編碼算法。此時直接對預測誤差用變字長編碼(VLC)壓縮碼率。無失真預測編碼框圖見圖1.4。
預測原理圖1.4 無失真預測編碼框圖
（2）有失真的預測編碼
通過量化器進行有失真的壓縮，達到比無失真預測編碼高得多的編碼效率，同時通過最佳非均勻量化器的設計，滿足一定的質量要求。這種編碼即為差分脈衝編碼調製DPCM。
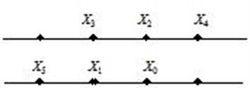
在對活動圖像預測編碼的套用中，大部分都是採用有量化的DPCM，以達到高壓縮比的要求。在預測時，採用當前像素附近的已經編碼傳輸的像素進行預測。圖1.5為當前像素 X與已編碼像素的位置關係。一般地，當把信號樣點與圖像中的位置聯繫起來後，可把DPCM分為以下幾類：
① X與 X位於同一幀圖像中的同一行，稱為一維預測。
② X為 X的同一幀中同一行及相鄰前幾行的像素，稱為二維預測。
③ X不僅有 X的同一幀 X已編碼的相鄰像素，還有相鄰前面幾幀的相鄰像素，稱為三維預測。
以上分類中，①和②只涉及到同一幀圖像內的像素，所以稱之為幀內預測，而③則還要考慮不同幀之間的像素，又稱之為幀間預測。
預測原理圖1.5 當前像素 X與已編碼像素的位置關係
