項鍊排序是組合數學中一個很常見的問題,可以在圓排列的基礎上求解。
·圓周排列:從n箇中取r個的圓排列的排列數為 P(n,r)/r , 2≤r≤n
·項鍊排列:正面向上和反面向上兩種方式放置各個數是同一個排列。因此,從n箇中取r個的項鍊排序數為
P(n,r)/2r, 3≤r≤n
項鍊排列生成算法
現在已經存在很多種全排列算法,例如字典序算法、遞增進位制算法、遞減進位制算法、鄰位對換法。這裡介紹一下項鍊排列生成的算法。我們不妨用1、2、...、n來表示n個元素
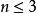 項鍊排列
項鍊排列對於 ,項鍊排列僅有一種。
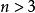 項鍊排列
項鍊排列對於 ,假設我們已經得到了n-1時的項鍊排列,我們由此序列來生成n的項鍊排列。
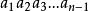 項鍊排列
項鍊排列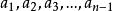 項鍊排列
項鍊排列假設 為n-1時的其中一個項鍊排列,那么我們可以將n分別插入到 後,由此生成新的n-1種排列
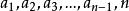 項鍊排列
項鍊排列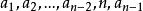 項鍊排列
項鍊排列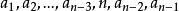 項鍊排列
項鍊排列......
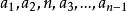 項鍊排列
項鍊排列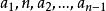 項鍊排列
項鍊排列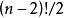 項鍊排列
項鍊排列對 個項鍊排列均進行此操作,即可生成一組新的一組排列,此排列即為n時的項鍊排列。
此算法與圓排列算法一致,只不過圓排列從n=3開始插值,而項鍊排列從n=4時插值。
算法正確性證明
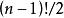 項鍊排列
項鍊排列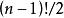 項鍊排列
項鍊排列 項鍊排列
項鍊排列首先我們由上述算法能夠得到,對於n,我們生成的排列有 中排列。與項鍊排列的個數相等,下面我們只需要證明這 個排列無重複即可。首先我們由上述構造方法可知, 一定為每個圓排列的頭。
下用數學歸納法證明:
1. 對於n=1,2,3,4時,無重複成立。
2. 假設對於n-1時,無重複成立。
3. 對於n時:
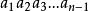 項鍊排列
項鍊排列由構造方式可知,n是採取插入的方式,故由 生成的n-1個序列中,n左右的兩個元素均不相同。故生成的n-1個序列兩兩不同。
 項鍊排列
項鍊排列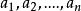 項鍊排列
項鍊排列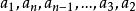 項鍊排列
項鍊排列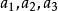 項鍊排列
項鍊排列下證由不同項鍊排列生成的序列無重複。因為 一定為每個項鍊排列的頭,所以若兩個序列重複,它們要么是完全相同的序列, 要么為 與 這樣的形式。(1234 1432為同一組項鍊排列)。但是,由於我們生成算法中不會改變的相對位置,(例如,將4插入序列123中,123的相對位置不變),故不可能出現以上情況。
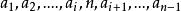 項鍊排列
項鍊排列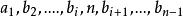 項鍊排列
項鍊排列故若序列 與序列 重複,兩者序列一定完全相同。那么去除n後,得到n-1的項鍊排列完全相同,這與假設矛盾,故對於n時生成的算法無重複。
即證。
