基本介紹
項鍊問題是一種圓排列問題，用r種不同顏色的珠子穿成項鍊，求所有不同的項鍊數。這個問題稱為項鍊問題。項鍊問題應解釋為第二種雙繞向圓排列。項鍊的珠子可以從r種顏色中允許重複任取n個，亦可以限定第i種顏色取b(i=1，2，…，r)個，
項鍊問題從而構成兩類不同問題(參見下文“圓排列”) 。
兩類項鍊問題的解
兩類項鍊問題的解如下：
1r種顏色珠子中允許重複任取n個所成不同的項鍊數
項鍊問題
項鍊問題這裡(k，x)表示k，x的最大公約數。
2.限定第i種顏色珠子取b個，i=1，2，…，r，
項鍊問題所成不同的項鍊數，可分下列各種情形計算：若
項鍊問題則當b中只有一例如b奇數，項鍊數
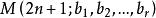項鍊問題
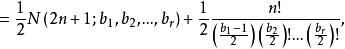項鍊問題當b中奇數多於一個時，
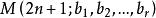項鍊問題
項鍊問題
項鍊問題
項鍊問題若b=2n，則當b全為偶數時，項鍊數
項鍊問題當b中恰有兩奇數，例如b，b為奇數，則
項鍊問題
項鍊問題當b中奇數多於兩個時，
項鍊問題以上式中的N(2n+1;b，b，…，b)和N(2n;b，b，…，b)為第二類手鐲數(參見“手鐲問題”) 。
圓排列
圓排列(circular permutation)是一類重要的排列，把若干元排列在圓周上，就構成了一個圓排列，這裡並不指定圓周上哪一個位置上的元處於首位，因此圓排列與線排列不同。
有兩種不同的圓排列：
第一種稱為單繞向圓排列：對圓周上元的排列順序，順時針與反時針視為不同，典型問題為手鐲問題。例如圓排列依順時針繞向有abcd，bcda，cdab，dabc，這四種(線)排列都表示同一個單繞向圓排列；但依反時針繞向有adcb，dcba，cbad，badc，則表示與前者相異的一個單繞向圓排列，用群的觀點說，這是在循環群作用下保持不變的圓排列。
第二種稱為雙繞向圓排列：對圓周上元的排列順序，順時針與反時針視為相同，典型問題為項鍊問題。如上例中八種(線)排列都表示同一個雙繞向圓排列，用群的觀點說，這是在兩面體群作用下保持不變的圓排列。
求給定約束條件下所有不同圓排列的個數，稱為圓排列問題，其基本形式有兩種：
1.求從r種相異元中可重複地任取n個元所組成的圓排列數。
2.求從r種相異元中任取n個元，滿足下述條件的圓排列數：第i種元恰有b(i=1，2，…，r)個且
項鍊問題一般地可用反演公式或伯恩賽德引理來求解圓排列問題 。
