簡介
評價水資源需要面平均雨量。雨量是分布得極不均勻的一種氣象要素。在大氣候環境相似的條件下,山區雨量多於平原,高地雨量多於河谷低地。雨量測點多數分布在平原和河谷,如簡單地求算術平均,是不能代表整個地區的真正面平均雨量的。於是,便發展了一些計算面雨量的方法。
計算方法
計算面平均雨量r的基本公式,是對各點實測雨量r以該點所代表的面積A作為權重的加權平均值:
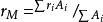 面平均雨量
面平均雨量以不同的方法決定Ai,就得到不同的面平均雨量計算方法。
泰森(Tiessen)法,實質上是多邊形面積法
出發點是使雨量站代表最靠近它的那塊地方。換句話說,在測站雨量r所代表的面積A內,任何一點與該雨量站的距離,比對於其他雨量站的距離都要近。將流域內每3個最靠近的雨量站連成一個三角形。流域邊緣的站可利用流域外相鄰的站來連線三角形。三角形的連法不是唯一的,應儘量使三個角比較均衡,不要相差太大。對各邊分別作垂直平分線,這些線構成若干多邊形,每個多邊形的面積為A。每個多邊形內只有一個雨量站,其雨量為r,代入上式,便可求得r。
三角形法
出發點是使雨量站代表它"周圍"的地方。也就是使測站雨量代表其周圍的幾個(個數不定)三角形的面積。做法如泰森法那樣,將相鄰的3個站連成三角形。任一二角形的面積為A,3個頂點是3個站,雨量分別為r、r、r,3個雨量的平均值是ri,代入上式即可。
等雨量線法
相鄰兩條等雨量線的標值的平均值是r,兩線之間的面積是Ai。代入上式即可。
雨量-高程法
如果雨量隨高程變化有良好關係,可以由高程推測雨量。先建立雨量r隨高程i變化的方程式。如果方程式不能適用於整個流域則應分區建立。從地圖上量出相鄰兩等高線之間的面積A,兩等高線標值的平均值是i。由雨量-高程關係求出相應的雨量是ri代入上式。
各種方法有其出發點和目標,也有其適用條件。
其他方法
還有距離和高程組加權法,趨勢面積分法,距離平方倒數法,改進多邊形法,有限單元法和變數分析法等。Sinh等曾利用美國新墨西哥州兩個區域和英國1個區域的雨量資料,對13種方法進行比較。他們認為在一定條件下有某一種方法比其他方法準確,不能籠統地說某種方法最好。
