無差別關係的性質
 無差別關係
無差別關係無差別關係具有下列性質( 是強優選關係G的補關係):
1.自反性:對任何a∈A,aIa。
2.對稱性:對任何a,b∈A,若aIb,則bIa。
3.傳遞性:對任何a,b,c∈A,若aIb,bIc,則aIc。
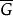 無差別關係
無差別關係 無差別關係
無差別關係4.對任何a,b∈A,若aIb,則a b且b a。
5.對任何a,b,c∈A,若aIb,且bGc, 則aGc。
6.對任何a,b,c∈A,若aIb,且cGa,則cGb。
7.對任何a,b,c,d∈A,若aGb且bIc且cGd,則aGd 。
相關介紹
為了描述優先關係,通常在數學上要用序(Order)的概念。序的概念涉及到二元關係 。
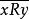 無差別關係
無差別關係設有一組元素x.y,z,...,w組成的集合X,在非空集X中的二元關係R,是X中所有有序對的乘積集X×X={(x, y)|x,y∈X}的一個子集。我們用xRy表示(x,y)有關係R(或記作(x,y)∈R),類似地用 表示(x,y)沒有關係(或記作(x,y)∈R)。二元關係有下述八種可能的性質,可分成四組。
自反性(reflexivity):xRx;
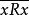 無差別關係
無差別關係非自反性(irreflexivity): ;
對稱性(Symmetry):若xRy,則yRx;
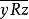 無差別關係
無差別關係非對稱性(asymmetry):若xRy,則 ;
可遞性(transitivity):若xRy和yRz,則xRz;
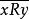 無差別關係
無差別關係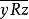 無差別關係
無差別關係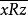 無差別關係
無差別關係負可遞性(negative transitivity):若 和 , 則 ;
連線性(connectedness):xRy或yRx;
弱連線性(weak connectedness):若x≠y,則有xRy或yRx 。
任意給定一個關係, 當然不可能同時具有上述性質,而只是其中一部分性質。其中某些性質如第一對性質不可能同時兼有,而後三對卻可以。例如具有非對稱和負可遞性就意味著有可遞性。有連線性就一定有弱連線性。當R是空集時,對稱性和非對稱性同時成立;但當R非空時,這兩個性質就不能兼有等等。例如,設X是所有居民的集合,“某高於某”的關係就具有非自反性、非對稱性、 可遞性和負可遞性。“某和某一樣年紀”的關係具有自反性、可遞性。“某和某是姐妹(至少父母中有一個是共同的)”的關係是對稱的, 但不一定是可遞的(除非要求父母都相同!)。
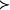 無差別關係
無差別關係 無差別關係
無差別關係可遞的二元關係稱為 序關係或有序。滿足上述某些性質的關係可以叫作各種序集。上述“年齡相同”是一種特殊的二元關係, 稱為 無差別關係。如果把“優先”作為原始的二元關係,就可以推出“無差別”及“優先或無差別”關係。符號 表示優先,~表示無差別, 表示優先或無差別。
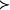 無差別關係
無差別關係若x y (讀為x優先於y)為原始的二元關係,則
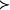 無差別關係
無差別關係 無差別關係
無差別關係x~ y,若且唯若非(x y) 以及非(y x);
 無差別關係
無差別關係 無差別關係
無差別關係 無差別關係
無差別關係 無差別關係
無差別關係x y,若且唯若x y,或非(x y)及非(y x)。
 無差別關係
無差別關係 無差別關係
無差別關係 無差別關係
無差別關係 無差別關係
無差別關係如果以 作為原始的二元關係,則它是非自反的,非對稱的,否則就會可能出現同時有y x及x y,還有x x,這都是不可能的 。

