基本定義
一個物體在另一個物體表面上具有相對運動趨勢時,所受到的阻礙物體相對運動趨勢的力叫靜摩擦力。這裡應注意三點:一是兩個緊密接觸而又相對靜止的物體;二是具有相對滑動或滾動的趨勢,但又還沒有發生相對的滑動或是滾動。 三是兩個物體必須是粗糙的。物體在斜面上也具有靜摩擦。
產生條件
①接觸面是粗糙的;
②兩個物體互相接觸且相互間有作用力;
③物體間有相對運動的趨勢;
④兩個物體相對靜止。
力的方向
①方向:靜摩擦的方向總是沿著接觸面,但當接觸面是曲面時,跟接觸面相切,並且跟物體相對運動趨勢方向相反。所謂的相對,是以施加摩擦力的施力物體為參考系的。
②相對運動趨勢的方向的判定:假設接觸面光滑沒有摩擦力,看物體的相對運動方向,由此判定相對運動趨勢的方向
力的大小
見圖2裝置,逐漸水平運動起來,於是,物塊與桌面間的靜摩擦力不復存在。由上面的分析可知:
①最大靜摩擦力:靜摩擦力存在最大值,稱為最大靜摩擦力。它等於使物體剛要運動所需要的最小外力。
②靜摩擦力的大小不是一個定值,靜摩擦力隨實際情況而變,大小在零和最大靜摩擦力Fm之間。其數值可由物體的運動狀態確定。最大靜摩擦力與接觸面壓力成正比,最大靜摩擦力隨壓力的增長而增長,隨壓力的減小而減小。
靜摩擦力是很常見的。如人走路就是受到向前的靜摩擦力的作用(人的腳跟相對於地面有向後的趨勢,腳跟一離地,沒有動力也就沒靜摩擦),如汽車的車輪,滾動摩擦實質上就是靜摩擦)靜摩擦力的大小只能根據物體現在所處的運動狀態(平衡或是加速),由平衡條件和牛頓定律來求解,與正壓力無關(與最大靜摩擦力不同)。例如,拿在手中的瓶子、毛筆不會滑落,就是靜摩擦力作用的結果。能把線織成布,把布縫製成衣服,也是靠紗線之間的靜摩擦力的作用。靜摩擦力在生產技術中的套用也很多。例如,皮帶運輸機是靠貨物和傳送皮帶之間的靜摩擦力把貨物送往別處。 還有,腳踏車、汽車主動輪與地面之間的摩擦力也屬於靜摩擦力,也就是說,滾動摩擦力也屬於靜摩擦力。
靜摩擦力
當外力加大到使物體開始移動的一瞬間,靜摩擦力增大到了最大值,稱為最大靜摩擦力。最大靜摩擦力與正壓力的大小有關,其值要略大於滑動摩擦力,但是有時候人們為了計算方便就認為最大靜摩擦力的大小等於滑動摩擦力的tactic 大小。
與拉力F大小相同、方向相反的力(有運動的趨勢的力),便稱靜摩擦力。
定義:兩個相互接觸,而又相對靜止的物體,在外力作用下如果只具有相對滑動趨勢,而又未發生相對滑動,則它們接觸面之間出現的阻礙發生相對滑動的力,謂之“靜摩擦力”。
大小:靜摩擦力隨著切向外力的增大而增大,但靜摩擦力的增大只能到達某一最大值。靜摩擦力f在,達到最大值以前總跟物體所受沿著接觸面切向方向的外力大小相等。
方向:達到最大值以前總是與相對滑動趨勢的方向相反
分析方法
1. 條件法
根據靜摩擦力產生的條件來判斷。這是分析靜摩擦力最直接、最基本的方法。
例1. 如圖1,在粗糙水平面上有一個三角形木塊,在它的兩個粗糙斜面上分別放有兩上質量為m1和m2的小木塊,m1>m2。已知三角形木塊和兩個小木塊都是靜止的,試分析粗糙水平面對三角形木塊的摩擦力。
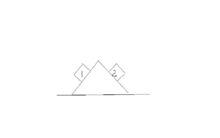 圖1
圖1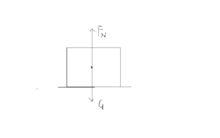 圖2
圖2分析 三角形木塊和兩個小木塊都靜止,則可將三者看成一個整體,如圖2。整體在豎直方向受到重力和水平面的支持力作用,合力為零;在水平方向沒有受到其它力的作用,沒有相對於水平面運動的趨勢,因此粗糙水平面對三角形木塊沒有靜摩擦力。
2.假設法
假設不存在靜摩擦力,分析物體將會發生怎樣的相對運動,從而確定靜摩擦力的作用效果。
例2. 如圖3,桿AB靜止地靠在直角牆上,牆的豎直部分光滑,水平部分粗糙,試分析桿受到的靜摩擦力。
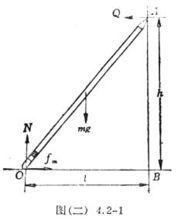 圖3
圖3分析 假設桿沒有受到靜摩擦力,那么桿的B端將會向右滑動,說明桿的B端受到水平向左的靜摩擦力作用,阻礙桿相對地面向右運動的趨勢。3. 平衡法
根據物體處於平衡狀態的條件來分析。
(1)利用共點力平衡條件:F合=0
例3. 如圖4,質量為m的物塊放在傾角為α的固定斜面上,物塊與斜面間的動摩擦因數為,物塊在一沿斜面向上的外力F作用下處於靜止狀態,求物塊和斜面間的摩擦力f。
分析 如圖5,物塊受到重力G、斜面的支持力N和外力F的作用。若物塊與斜面間有摩擦力,則為靜摩擦力。要確定物塊相對於斜面的運動趨勢,應先確定外力F與重力沿斜面的分力mgsinα的大小關係。由於F大小未知,利用共點力平衡條件討論如下:
①若F=mgsinα,物塊與斜面間沒有相對運動趨勢,所以物塊和斜面間沒有摩擦力。
②若F>mgsinα,物塊相對於斜面有向上的運動趨勢,斜面對物塊的靜摩擦力方向沿斜面向下,並且有F=mgsinα+f,即
f=F-mgsinα
③若F<mgsinα,物塊相對於斜面有向下的運動趨勢,斜面對物塊的靜摩擦力方向沿斜面向上,並且有F+f=mgsinα,即
f=mgsinα-F。
(2)利用力矩平衡條件:M合=0
例4. 如圖6,不可伸長的輕繩將一個均勻的、重為G的球懸於豎直牆上的A點,球靜止,繩系在球上的C點。試分析球與豎直牆面間的靜摩擦力方向。
分析 分析球的受力如圖7。以球心為支點,合力矩為零。其中,重力G和支持力N均過球心,力矩為零,所以,靜摩擦力的力矩與繩子拉力的力矩大小相等、方向相反,因此B處的靜摩擦力方向一定豎直向上,產生逆時針方向力矩,與繩的拉力T產生的順時針力矩平衡。
4. 利用牛頓第二定律分析
例5. 如圖8,A、B兩物體疊放在固定的光滑斜面上共同下滑,求B受到的靜摩擦力。
分析 先以A、B整體為研究對象,因為斜面光滑,所以A、B共同下滑的加速度a=gsinθ。
再以物體B為研究對象,它的加速度也為a。如圖9,將a沿水平方向和豎直方向分解為ax、ay。分析B的受力,由牛頓第二定律可知,重力與支持力的合力產生了豎直方向的加速度ay,而水平方向的加速度ax應由水平向左的靜摩擦力產生,所以
方向向左。
5. 利用牛頓第三定律分析
例6. 如圖10,在力F的作用下,質量均為m的A、B兩物體均靜止,試分析A受到的靜摩擦力。
分析 直接隔離A很難分析其受力情況。可先隔離B,如圖11,可知A對B的靜摩擦力和B的重力是一對平衡力,即A對B的靜摩擦力fAB=mg,方向豎直向上。根據牛頓第三定律得,B對A的靜摩擦力fBA=mg,方向豎直向下,由於A處於平衡狀態,由平衡條件可知,A還受到牆對它的靜摩擦力F=2mg,方向豎直向上。
小結靜摩擦力的分析方法多且活,要根據具體問題的特點選擇適當的方法。以上方法的運用往往不是獨立的,要注意聯繫和有機結合。

