定義
電報方程又名傳輸線方程，是描述傳輸線上任意點電壓、電流與傳輸線一次參數之間關係的微分方程組。
發現
在溝通大西洋電纜(海底電纜)時，開爾文首先發現了長線效應：即當傳輸線長與電報信號的波長可比擬或者超過波長時，我們必須計算其波動性，這時傳輸線也稱長線，而電報信號的反射、傳輸都與低頻也有很大的不同。開爾文研究電纜中信號傳播的情況，得出了信號傳播速度減慢與電纜長度平方成正比的規律。
電報方程公式
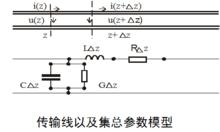電報方程為了研究無限長傳輸線的支配方程，定義電壓 u 和電流 i 均是距離和時間的函式，即
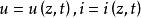電報方程利用基爾霍夫定律可得：
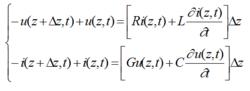電報方程當Δz→0時，上面的方程就會變成微分方程：
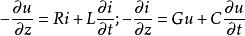電報方程上式是均勻傳輸線方程或電報方程。
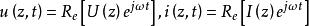電報方程當正弦信號施加於均勻傳輸線時，電壓和電流為 。 U(z)、I(z)只與z有關，表示在傳輸線z處的電壓或電流的有效復值。電報方程則變成下列形式：
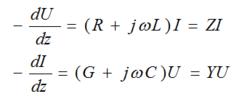電報方程式中R、C、G、L是傳輸線的一次參數，ω是信號的角頻率，dz是傳輸線的一個微分長度。第一個方程表示信號電壓沿傳輸方向的增長率是負的。第二個方程表示電流沿傳輸方向也是不斷減小的。通過上式可知電壓的空間變化是由電流的時間變化產生的，電流的空間變化是由電壓的時間變化產生的。
對上式加以變化，又可變為：
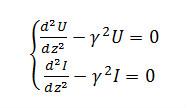電報方程
電報方程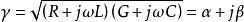式中，
電報方程
電報方程稱為傳輸線的傳輸係數，稱為衰減係數，β為相移係數。
由上式電報方程可以看出，在傳輸線上，電壓和電流是以波的形式傳播。
