發展背景
計算機性能的飛速提升和流體力學數值計算方法的迅速發展，為計算流體力學(CFD)的發展提供了必要的前提條件，從而奠定了計算流體力學(CFD)在國民經濟中的重要地位。計算流體力學已經發展成為“解決氣象、交通、建築、橋樑和生命科學等多領域中流體力學問題”的強有力工具。尤其在航空、航天領域，計算空氣動力學已經與實驗空氣動力學一起被視作空氣動力學兩大並列的分支，它們互相補充，互相驗證，共同發展進步。計算流體力學是多領域交叉的綜合性學科，涉及計算機科學、流體動力學、偏微分方程的數學理論、計算幾何、數值分析等多方面;這些學科交又融合，相互促進和支持，又推動了這些學科的深入發展。
在近三十年來，隨著速勢方法、求解Euler方程方法以及Euler方程與附面層方程耦合疊代方法等數值求解技術的不斷發展和完善，計算流體力學己經可以像實驗一樣十分逼真地模擬真實的流動過程，從而部分取代了實驗研究，在工程套用領域中有著不可替代的作用。然而對於某些複雜的粘性繞流，如強激波/附面層相互干擾、大迎角分離流動、旋渦的形成與發展等問題，上述方法則顯得力不從心，所以人們逐步發展了Navier-Stokes困S)方程的數值求解技術。以前由於受到計算機的限制，對複雜外形的粘性繞流的NS方程求解，發展相對緩慢。在近幾年時間裡，得益於計算機技術的發展，已經可以利用計算機求解NS方程，模擬複雜外形飛行器的粘性繞流。
現代飛行器設計要求我們採用的數值方法儘可能精確的模擬流場的粘性效應，以準確地預測各種外形飛行器的氣動力特性。引入湍流模型計算雷諾平均的NS方程(RANS)，是目前數值模擬複雜粘性流場的主要方法，加入湍流模型後的RANS方程在計算升力、阻力、力矩方面的精度能得到極大提高。
湍流
湍流是流體的一種流動狀態。當流速很小時，流體分層流動，互不混合，稱為層流，也稱為穩流或片流；逐漸增加流速，流體的流線開始出現波浪狀的擺動，擺動的頻率及振幅隨流速的增加而增加，此種流況稱為過渡流；當流速增加到很大時，流線不再清楚可辨，流場中有許多小漩渦，層流被破壞，相鄰流層間不但有滑動，還有混合,形成湍流，又稱為亂流、擾流或紊流。
在自然界中，我們常遇到流體作湍流，如江河急流、空氣流動、煙囪排煙等都是湍流。
湍流是在大雷諾數下發生的，雷諾數較小時，黏滯力對流場的影響大於慣性力，流場中流速的擾動會因黏滯力而衰減，流體流動穩定，為層流；反之，若雷諾數較大時，慣性力對流場的影響大於黏滯力，流體流動較不穩定，流速的微小變化容易發展、增強，形成紊亂、不規則的湍流流場。
湍流基本特徵是流體微團運動的隨機性。湍流微團不僅有橫向脈動，而且有相對於流體總運動的反向運動，因而流體微團的軌跡極其紊亂，隨時間變化很快。湍流中最重要的現象是由這種隨機運動引起的動量、熱量和質量的傳遞，其傳遞速率比層流高好幾個數量級。
定義
雷諾平均方程是描述湍流統計量的演化的系綜平均N-S方程。
納維-斯托克斯方程
納維-斯托克斯方程(英文名;Navier-Stokes equations)，描述粘性不可壓縮流體動量守恆的運動方程。簡稱N-S方程。粘性流體的運動方程首先由Navier在1827年提出，只考慮了不可壓縮流體的流動。Poisson在1831年提出可壓縮流體的運動方程。Saint-Venant在1845年，Stokes在1845年獨立提出粘性係數為一常數的形式，現在都稱為Navier-Stokes方程，簡稱N-S方程。在直角坐標系中，其矢量形式為=-Ñp+ρF+μΔv。
納維-斯托克斯方程(Navier-Stokes equation)描述粘性不可壓縮流體動量守恆的運動方程，簡稱N-S方程。此方程是法國科學家C.-L.-M.-H.納維於1821年和英國物里學家G.G.斯托克斯於1845年分別建立的，故名。
雷諾平均方程簡介
雷諾平均NS 方程是流場平均變數的控制方程，其相關的模擬理論被稱為湍流模式理論。湍流模式理論假定湍流中的流場變數由一個時均量和一個脈動量組成，以此觀點處理NS 方程可以得出雷諾平均NS 方程（簡稱RANS 方程）。再引入Boussinesq 假設，即認為湍流雷諾應力與應變成正比之後，湍流計算就歸結為對雷諾應力與應變之間的比例係數（即湍流粘性係數）的計算。正是由於將控制方程進行了統計平均，使得其無需計算各尺度的湍流脈動，只需計算出平均運動，從而降低了空間與時間解析度，減少計算工作量。根據計算中使用的變數數目和方程數目的不同，湍流模式理論中所包含的湍流模型又被分為二方程模型、一方程模型和零方程模型（代數模型）等大類。FLUENT 中使用的三種k −ε模型、Spalart-Allmaras 模型、k −ω模型及雷諾應力模型（RSM）等都屬於湍流模式理論。雷諾平均模型的主要缺點是它只能提供湍流的平均信息，這對於近代自然環境的預報和工程設計是遠遠不夠的；雷諾平均模型的致命弱點是它的模型沒有普適性。
RANS方程表達式
空氣的可壓縮RANS方程可以寫成採用求和約定的笛卡兒張量形式。
連續方程：
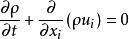雷諾平均方程動量方程：
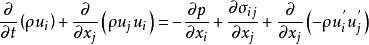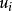雷諾平均方程
雷諾平均方程
雷諾平均方程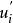
雷諾平均方程
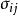雷諾平均方程其中 表示略去平均符號的雷諾平均速度分量， 為密度，p為壓強， 為脈動速度， 為應力張量分量。
優缺點
預測湍流的統計量的湍流統計理論或其他基礎研究在近期內還看不到突破的希望，受計算機水平的限制，從NS方程出發對湍流進行直接數值模擬(DNS)，難以解決工程中遇到的複雜湍流問題，依靠實驗取得經驗數據，不僅耗資巨大，周期很長，而且對於某些實際工程問題，完全相似的實驗室模擬不可能實現。在這種情況下，求解雷諾平均的NS方程(RANS)方法成為解決工程問題比較有效、切實可行的手段。
但RANS方法也有它的缺陷:在平均運動中湍流脈動量的影響即雷諾應力是未知的，需要建立湍流模型。所謂湍流模型，就是以雷諾平均NS(RANS)方程與脈動方程為基礎，依靠理論與經驗的結合，引進一系列模型假設，建立一組描寫湍流平均量的封閉方程組的理論計算方法。雷諾應力的主要貢獻來自大尺度脈動，而大尺度脈動的性質及結果和流動的邊界條件密切相關，因此雷諾應力的封閉模型不可能是普適的，就是說，不存在對一切複雜流動都適用的統一封閉模型。
