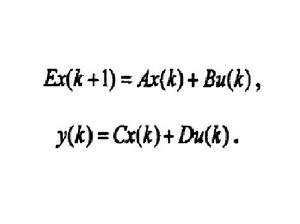基本概念
廣義系統，又稱為奇異系統、微分代數系統或隱式系統，可分為微分方程描述的連續廣義系統和用差分方程描述的離散廣義系統兩類。
因廣義系統能更加近似的模擬電力、航空航天和社會經濟等實際系統，所以近年來對廣義系統的研究十分活躍。而穩定性和控制器設計作為廣義系統研究中的重中之重，更加受到學者的關注，伴隨著計算機技術的日亦發展及其相應理論在實際工程系統中套用的日趨深入，而計算機又只能讀取離散信號，所以離散廣義系統逐漸成為現代控制理論研究的熱點。
研究現狀
對離散廣義系統的研究大體可分為兩個階段：
（1）基於傳統理論的離散廣義系統的普通控制器的研究；
（2）基於現代理論的離散廣義系統的智慧型控制器的研究。
普通控制器理論及其發展為我們所熟知，並且已經趨於成熟。第二個階段，由於T-S模糊控制方法在經典系統的穩定性研究中的日益完善，研究人員通過將正常系統的T-S模糊的理論方法引入到廣義系統，建立起廣義系統的T-S模糊控制方法，使得廣義系統的模糊控制方面的研究得到了迅速的發展。更進一步，將其推廣到廣義離散時間系統中來，以完善廣義離散時間系統的T-S模糊控制理論，從而也推動了智慧型控制的發展。
雖然國內外有關離散廣義系統的穩定性和控制器設計已取得豐碩的研究成果，但依然有許多的研究領域需要我們進一步去探索，有待我們去解決和進一步的開拓。
表達形式
通常離散廣義系統可以表達為如下形式：
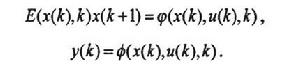離散廣義系統其中，u(k)∈R，是控制輸入，x(k)∈R”是系統狀態向量，y(k)∈R是系統輸出，φ和Φ是有關x(k)，u(k)，k的函式，E(x(k),k)∈R是函式矩陣。當rankE=n和rankE=r<n時，上式分別稱為經典離散系統和離散奇異（廣義）系統，若φ(x(k)，u(k)，k)是非線性形式時，上式表示為非線性離散廣義系統；當φ(x(k)，u(k)，k)是線性形式時，式上是一個線性離散廣義系統，其表達式可以化為如下形式：
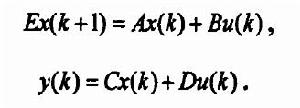離散廣義系統此時E，A，B，C，D分別是具有相應維數的定常矩陣。
穩定性分析
離散廣義系統的能控性與穩定性
考慮如下離散廣義系統（1）：
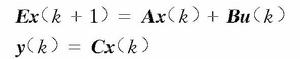離散廣義系統假設u(k)=0，取如下形式的廣義Lyapunov函式
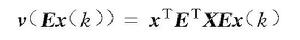離散廣義系統於是有
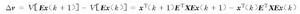離散廣義系統可以得到
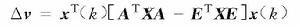離散廣義系統如果令
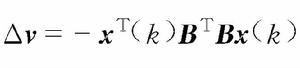離散廣義系統則得到如下的廣義Lyapunov方程
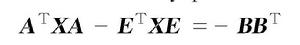離散廣義系統由rank(E)=r<n，總存在可逆陣P1,Q1使得
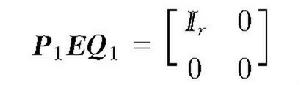離散廣義系統假設X為對稱矩陣，則
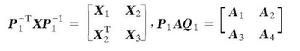離散廣義系統
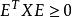離散廣義系統
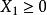離散廣義系統由 得 ，則有
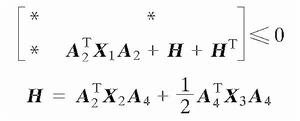離散廣義系統於是
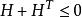離散廣義系統當
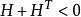離散廣義系統有
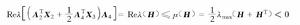離散廣義系統 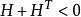離散廣義系統假設滿足 的廣義系統是能控的，下列命題等價：
（1）存在對稱矩陣X滿足如下廣義Lyapunov方程及約束
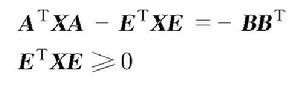離散廣義系統（2）系統（1）是容許的。
離散廣義系統的能觀性與穩定性
取如下形式的廣義Lyapunov函式
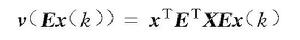離散廣義系統則
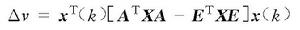離散廣義系統令
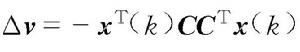離散廣義系統則得到如下的廣義Lyapunov方程
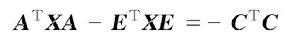離散廣義系統 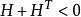離散廣義系統假設滿足式 的廣義系統（1）是能觀的，下列命題等價：
（1）存在對稱矩陣X滿足如下廣義Lyapunov方程及約束
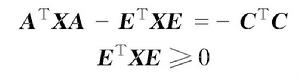離散廣義系統（2）系統（1）是容許的。
離散廣義系統的T-S模糊穩定性
因為廣義系統能更加近似的模擬電力、航空航天和社會經濟等實際系統，所以近年來對廣義系統的研究十分活躍。而穩定性和控制器設計作為廣義系統研究中的重中之重，更加受到學者的關注。T-S模糊控制系統理論，自1974年提出以來，一直是模糊控制領域最活躍的一個分支。近年來，許多學者將其運用到連續時間系統、離散時間系統和廣義連續時間系統中。
考慮下面的離散T-S模糊廣義系統模型，其第i條模糊規則可表示為如下形式
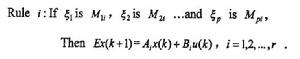離散廣義系統離散廣義模糊系統的全局模型：
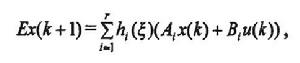離散廣義系統
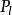離散廣義系統
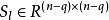離散廣義系統對輸入採用雙交疊模糊分劃的離散T-S模糊廣義系統，其正則、因果、穩定的充分條件是在各最大交疊規則組中分別存在正定矩陣 和對稱矩陣 滿足下式：
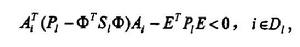離散廣義系統