概述
按圖像的點空間位置和灰度大小變化的方式,圖像可分為連續圖像和離散圖像兩類。
所謂連續圖像是指在二維坐標系中具有連續變化的空間位置和灰度值的圖像。連續圖像一般為光強度(或亮度)對空間坐標的函式。在用計算機對其處理之前,必須用圖像感測器將光信號轉換成表示亮度的電信號,再通過模數轉換器(A/D)量化成離散信號以便於數字計算機進行各種處理。從位置上看,圖像中的所有元素都在一個平面內,像元在二維方向上連續分布;從原稿某一點位置的亮度來看,其取值也是連續分布的,即像元的亮度是像元位置的函式。其典型代表是由光學透鏡系統所獲取的圖像,如彩色照片、航攝相片等,用眼睛觀測連續圖像時無不自然感覺。
離散圖像是以一定格線為周期,把X,Y坐標軸劃分為棋盤式的格線,僅取離散的各個交點位置上的灰度值,構成的圖像稱為離散圖像,也稱採樣圖像。印刷圖像其實就是離散圖像,電腦圖像和掃描圖像都是離散圖像。
離散圖像在空間位置上是被分割成一個個的點,在灰度值的大小上也分為不同級數的圖像。
數字圖像就是離散圖像,數字圖像是一組有序排列的數據集合,需要用圖像數位化設備獲得。圖像的數位化包含兩個方面的內容:空間位置的離散和數位化以及亮度的離散和數位化。可以認為,空間位置的離散為抽樣,而亮度的數位化則是量化。
離散圖像變換
圖像一般是以連續形式出現的,我們常常採用連續圖像的離散表達形式進行分析處理,所以許多數字圖像處理步驟要求我們在處理這些離散數據時要時刻考慮到採樣和插值的問題。然而,有一些套用卻允許我們將數字圖像看作原本就是離散的。離散圖像的變換有離散傅立葉變換(DFT),Walsh變換、離散K—L變換、Hadamard變換等。下面以離散傅立葉變換(DFT),Walsh變換、離散K—L變換和Hadamard變換為例進行詳細解釋。
離散傅立葉變換(DFT)
連續傅立葉變換不適用於計算機的處理,而離散傅立葉變換由於其輸入和輸出都是離散值,故方便計算機的計算,且可以用快速傅立葉變換進行計算,以提高計算速度。
(1)一維離散傅立葉變換
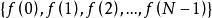 離散圖像
離散圖像 離散圖像
離散圖像設 為一維信號 的N個採樣,由式(1)和式(2)可知,則可將離散傅立葉變換對定義為
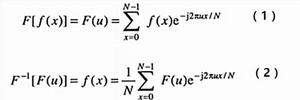 離散圖像
離散圖像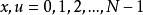 離散圖像
離散圖像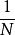 離散圖像
離散圖像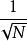 離散圖像
離散圖像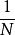 離散圖像
離散圖像式中, 。式(2)中的係數 也可以放在式(1)中,有時也可在傅立葉正變換和逆變換前分別乘以 ,這是無關緊要的,只要正變換和逆變換前係數乘積等於 即可。
根據式(1),一維DFF可以表達為如下的矩陣形式:
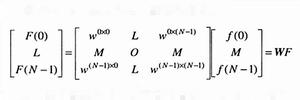 離散圖像
離散圖像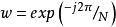 離散圖像
離散圖像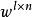 離散圖像
離散圖像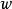 離散圖像
離散圖像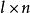 離散圖像
離散圖像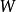 離散圖像
離散圖像 離散圖像
離散圖像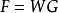 離散圖像
離散圖像式中, ,稱為旋轉因子, 表示 的 次方。常用一維DFT的核矩陣 是對稱矩陣,設 為一維信號矩陣,可將上式所示的一維離散傅立葉變換(DFT)用矩陣的形式表示為 。
同樣,很容易將一維離散傅立葉變換推廣N--維情況。二維離散傅立葉變換對定義為
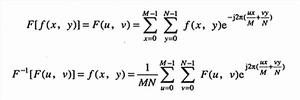 離散圖像
離散圖像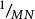 離散圖像
離散圖像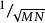 離散圖像
離散圖像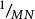 離散圖像
離散圖像式中:x、u=0,1,2,...,M-1,y、v=0,1,2,...,N-1。與一維離散傅立葉變換類似,係數 可以在正變換或逆變換中,也可以在正變換和逆變換前分別乘以係數 ,只要兩式係數的乘積等於 即可。
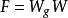 離散圖像
離散圖像同樣,二維傅立葉變換也可以寫成矩陣形式:
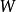 離散圖像
離散圖像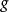 離散圖像
離散圖像其中, 為傅立葉變換核矩陣, 為二維信號矩陣。
Walsh變換
離散傅立葉變換和離散餘弦變換雖然都有快速算法,但它們都用到了複數乘法,使得計算機在運算時將實、虛部分開運算,所以速度仍比較慢。基於以上原因,許多學者設法找到另一種運算簡單的正交變換,即計算簡單、矩陣產生方便且正交完備。Walsh變換就是其中一種,它的主要優點在於矩陣產生容易,需要的存儲空間小,運算速度快,特別是在大量數據需要實時處理時,Walsh函式就更加顯示出它的優越性了。
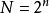 離散圖像
離散圖像對於一個 的離散序列,一維離散Walsh變換可用式(1)和式(2)表示:
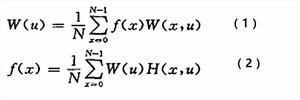 離散圖像
離散圖像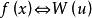 離散圖像
離散圖像形成Walsh變換對:。
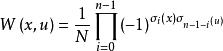 離散圖像
離散圖像其中,離散Walsh變換核
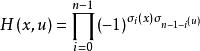 離散圖像
離散圖像離散Walsh反變換核
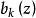 離散圖像
離散圖像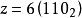 離散圖像
離散圖像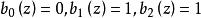 離散圖像
離散圖像是2的二進制表達中的第k位,例如,n=3時,則對 ,有 。
二維離散Walsh變換可以寫成
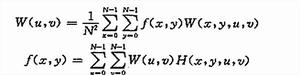 離散圖像
離散圖像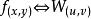 離散圖像
離散圖像形成Walsh變換對,記作 。
離散K—L變換
K-L變換是由Karhunen和Loeve兩人對連續隨機過程作為級數展開而引出的。隨機圖像序列是由Hotelling首先研究出的一種主分量方法,實際上它是K—L級數展開的離散等效方法。因此這種方法有很多稱謂,如K-L變換、Hotelling變換、特徵向量變換、主分量變換等。這種變換不像上述的各種變換,那些變換的變換核是固定不變的,而K—L變換則隨各種圖像的統計性質不同而有不同的變換核矩陣,即變換核矩陣是由某批圖像的統計性質來確定的。例如遙感多光譜圖像對同一地區有多幅光譜圖像,每一幅圖像是在特定光譜波長拍攝的,這樣就可進行統計;又如一幅圖像通過衛星傳送了N次,由於電波傳播的影響,N幅圖像互有差異,這樣也可進行統計。
Hadamard變換
Hadamard變換是一種獨特有趣的變換.其變換核是一個所有元素為+1或-1的Hadamard矩陣,這顯然意味著Hadamard變換不需要乘法運算。Hadamard矩陣具有許多有趣的性質,下面我們給出Hadamard矩陣的基礎理論, 然後繼續給出變換的定義。
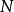 離散圖像
離散圖像 離散圖像
離散圖像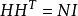 離散圖像
離散圖像定義:邊長 的Hadamard矩陣 是一個N×N的矩陣,其元素都是±1並具有如下性質: 。
因此Hadamard矩陣是正交的,這是一個圖像變換中期望的性質,Hadamard的正交特性帶來了以下的結果。
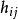 離散圖像
離散圖像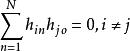 離散圖像
離散圖像(1)元素為 的N X N矩陣是Hadamard陣的充分必要條件是: 。
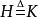 離散圖像
離散圖像 離散圖像
離散圖像(2)令K和L分別為邊長為N和R的Hadamard矩陣,則 ⊗ 也是一個Hadamard矩陣。
(3)邊長N的矩陣是Hadamard陣,則N是1,2或4的倍數。
(4)H是一個Hadamard陣,如果矩陣K是通過下列方法之一從H中獲得,則K也是一個Hadamard陣。
(a)對部分或所有行取反;
(b)對部分或所有列取反;
(c)對行或列變換次序。
離散圖像濾波
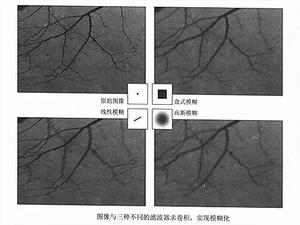 離散圖像
離散圖像也許最簡單的卷積套用是用離散卷積處理圖像。圖像運算程式中 ,得到最廣泛套用的是簡單的卷積濾波器。通過與一般低通濾波器(從盒式濾波器到高斯濾波器)進行卷積,實現對圖像的模糊化處理,如右圖所示。高斯濾波的結果看起來很平滑,所以經常用它進行模糊化處理。
 離散圖像
離散圖像與圖像模糊化相對的運算是圖像銳化。實現銳化的一種方式是採用“模糊掩模”:從原始圖像中減去一幅模糊化圖像的一部分 。重新調整尺度,以免圖像的整體亮度發生改變。於是有:
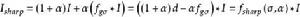 離散圖像
離散圖像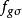 離散圖像
離散圖像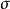 離散圖像
離散圖像其中 是寬度為 的高斯濾波器。利用離散脈衝趿卷積的分配律,可以把整個過程表示為含模糊寬度及銳化程度兩個參數的單一濾波器。
另一個結合使用兩離散濾波器的實例是陰影。通常利用模糊的、移位的目標輪廓來構造柔和的陰影。可以將移位運算表示為與偏離中心的一個脈衝的卷積:
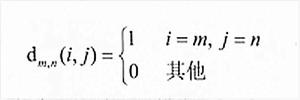 離散圖像
離散圖像通過與兩種濾波器的卷積運算,就實現了移位及模糊化:
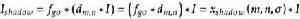 離散圖像
離散圖像上式中利用了結合律,將兩次運算合成,變成含三個參數的一個濾波器。

