定義
在理想溶液中，溶液組分i遵循拉烏爾定律：
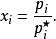離子活度係數
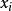離子活度係數
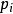離子活度係數
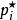離子活度係數
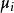離子活度係數其中 是組分i在溶液中的摩爾分數， 和 分別是組分i的分壓和飽和蒸氣壓。 而組分i的化學勢 可由下式表達：
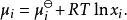離子活度係數
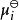離子活度係數這裡的 代表組分i在標準狀態下的化學勢。而在真實溶液中，組分i-組分i間的作用力和組分i-其他組分間的作用力並不相等，導致了組分i並不滿足拉烏爾定律，其化學勢也不滿足以上關係，即偏離了理想溶液的行為，為此吉爾伯特·牛頓·路易斯引入了活度和活度係數的概念。 定義：
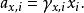離子活度係數
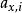離子活度係數
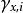離子活度係數這裡的 是組分i以摩爾分數所表示的活度， 則是組分i用摩爾分數所表示的活度係數。引入活度和活度係數後，拉烏爾定律可以修正為：
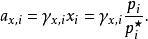離子活度係數組分i的化學勢則可以修正為：
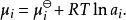離子活度係數真實溶液的濃度越稀，溶劑的活度係數就越接近1，活度和摩爾分數近乎相等，其行為越接近理想溶液。濃度越高，活度係數越偏離1，真實溶液的行為偏差理想溶液就越大，比如對於濃度較高的電解質溶液，其活度就無法用摩爾分數取代，這一點在電化學和土壤化學中十分常見。
平衡常數修正
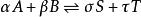離子活度係數當化學反應: 達到化學平衡時，反應物化學勢的和等於生成物化學勢的和，反應的吉布斯能變化{\displaystyle \Delta _{r}G}為0，即：
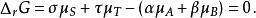離子活度係數將每種物質用活度所表示的化學勢表達式代入其中得到
離子活度係數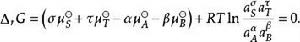
離子活度係數
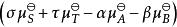離子活度係數
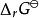離子活度係數其中的 是反應在標準狀況下的吉布斯能變化
於是
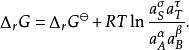離子活度係數
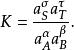離子活度係數此時的平衡常數由平時的 修正為：
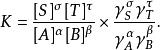離子活度係數測量和計算
活度係數可以通過實驗測量和理論計算結合的方法求出，常見方法有蒸氣壓法、德拜-休克爾極限公式法、圖解積分法和測量電動勢法等：
蒸汽壓法
引入活度係數後，拉烏爾定律修正為：
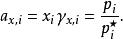離子活度係數可通過測定某一濃度下溶液蒸汽壓和飽和蒸汽壓的比值，除以其摩爾分數，即為活度係數。
德拜-休克爾極限公式法
德拜-休克爾極限公式給出了某種離子i的活度係數和離子強度的關係：
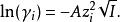離子活度係數
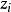離子活度係數
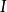離子活度係數其中 是離子所帶的電荷數， 是溶液中的離子強度，A是和溶劑有關的常數。 但德拜-休克爾極限公式只適用於稀溶液，對於較高濃度的電解質溶液，需要使用戴維斯公式或pitzer公式等修正後的方法。
圖解積分法
對於雙組分溶液，根據吉布斯-杜安方程，於恆壓P和恆溫T下
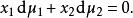離子活度係數根據用活度係數表示的化學勢
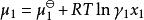離子活度係數可得
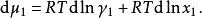離子活度係數代入吉布斯-杜亥姆方程：
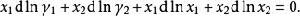離子活度係數注意到
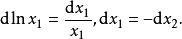離子活度係數所以
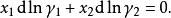離子活度係數這樣，在已知其中一種組分的活度係數之後，可以通過積分求出另一種活度係數，或用這一關係檢驗所測得的活度係數數值是否具有熱力學一致性。
相關條目
•活性度
