定義
 雙周期函式
雙周期函式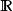 雙周期函式
雙周期函式對一個定義域為複數域 的函式 f來說,如果存在兩個在實數域 上線性獨立(將複數域看作實數域上的2維向量空間)的複數 u和 v,使得對任何複數 z以及任何整數 m, n,都有:
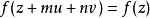 雙周期函式
雙周期函式就稱函式 f為雙周期函式。
復變數函式中有單周期函式和雙周期函式。單周期函式可以看作是第二個周期為無窮大的雙周期函式。而三周期或更多周期的函式是不存在的,因為複平面是實數域的二維向量空間,所以不可能有三個或更多個線性獨立的向量(複數)。
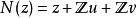 雙周期函式
雙周期函式 雙周期函式
雙周期函式給定雙周期函式 f,對每個複數 z,可以確定函式值等於 f( z)的複數包括如下集合: ,其中的 表示整數集。這個集合 N( z)在平面上呈一個格線狀的結構,將複平面劃分為一個個平行四邊形形狀的格子,稱為單元格。雙周期函式的定義表明,函式在每個單元格中有相同的形狀。
例子
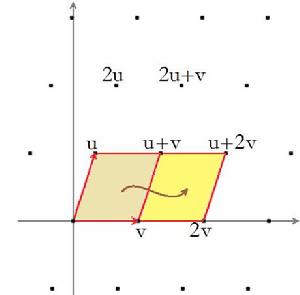 雙周期函式
雙周期函式只要將雙周期函式在某個單元格中定義,就可以推出函式在其它“格子”里的值。
 雙周期函式
雙周期函式如果將雙周期函式直觀地作為二維平面上的一類實值函式來看待的話,很容易就能構造出雙周期函式的例子。比如,如果將“1”和“ i”作為周期,那么對應的格線是以平面上所有的“整點”(橫坐標和縱坐標都是整數的點)為節點的正方形格線。只需要定義函式在一個正方形單位上的取值,然後再“逐格複製”就可以了。例如函式:
從例子中可以看出,定義一個雙周期函式,只需要定義它在一個單元格里的取值就可以了。如果 u和 v是雙周期函式 f的周期,那么只需要定義 f在集合:
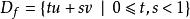 雙周期函式
雙周期函式(一個平行四邊形)上的取值即可。
函式舉例
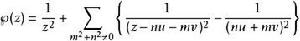 雙周期函式
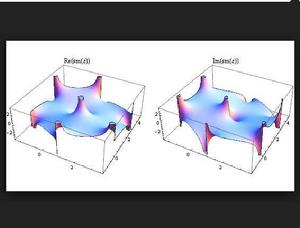
雙周期函式橢圓函式是雙周期函式中最常被研究的一類函式。橢圓函式定義為雙周期的亞純函式(在離散的點以外都是全純函式的函式)。一個常見的例子是魏爾斯特拉斯橢圓函式:
性質
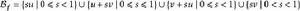 雙周期函式
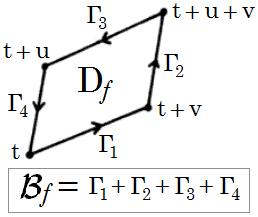
雙周期函式設單元格 D的邊界為 B。 B由四條首尾相連的直線段構成:
沿著雙周期函式單元格的環路積分。
 雙周期函式
雙周期函式由於雙周期函式 f在兩條平行邊上的取值一樣(周期性),如果以 B為路徑對函式 f進行環路積分,積分值會是0:
如果 f是全純函式,那么可以證明, f是常數函式: f≡ C. 這是因為 f在單元格上的取值是必定是有界的(單元格是緊集),所以根據雙周期性可知 f在整個平面上都是有界的函式。因此根據劉維爾定理, f是常數函式。
如果 f是橢圓函式,那么根據留數定理, f在單元格內極點的留數之和等於0,這說明 f在單元格里不可能只有一個一階極點。要么有一個留數是0的高階極點,要么有多於一個一階極點。 同樣地,對橢圓函式函式1/ f使用留數定理,可以證明 f在單元格里不可能只有一個一階零點。要么有一個高階零點,要么有多於一個一階零點。更進一步地,可以證明 f在單元格內取得每個值的次數等於它在單元格內的階數(橢圓函式在某個區域內的階數等於它的所有極點的階數和)。
 雙周期函式
雙周期函式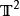 雙周期函式
雙周期函式從拓撲結構來說,任何雙周期函式都等價於定義在環面上的函式。所以以上的性質也對定義在環面上的函式適用。