定義[編輯]
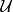集合覆蓋問題
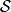集合覆蓋問題 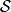集合覆蓋問題給定全集 ，以及一個包含n個集合且這n集合的並集為全集的集合 。集合覆蓋問題要找到的一個最小的子集，使得他們的並集等於全集。
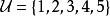集合覆蓋問題
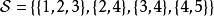集合覆蓋問題 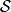集合覆蓋問題 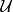集合覆蓋問題 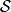集合覆蓋問題
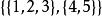集合覆蓋問題例如，，雖然中所有元素的並集是}，但是我們可以找到的一個子集，我們稱其為一個集合覆蓋。
集合覆蓋問題 集合覆蓋問題
集合覆蓋問題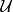 集合覆蓋問題形式化的定義，給定全集和他的一組子集組成的集合， 覆蓋指一個集合且C的元素的並集為。
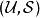集合覆蓋問題 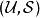集合覆蓋問題集合覆蓋問題的決定性問題為，給定和一個整數k，求是否存在一個大小不超過k的覆蓋。集合覆蓋的最佳化問題為給定，求使用最少的集合的一個覆蓋。
決定性問題的集合覆蓋是NP完全問題，最佳化問題的集合覆蓋是NP困難問題。
此外，問題可以在每個集合上添加權值而變為帶權集合覆蓋問題。
簡介
經典SCP描述包含一個集合U以及U內元素構成的若干各小類集合S，目標是找到S 的一個子集，該子集滿足所含元素包含了U中的所有的元素且使小類集合個數最少。例如，U={1,2,3,4,5}，S={{1,2},{3,4},{2,4,5},{4,5}},找到集合能滿足條件的可以有O={{1,2},{3,4}{4,5}}或是O={{1,2},{3,4},{2,4,5}}，至於具體選哪種組合，還有引申的一個問題：WSC，即Weighted Set Cover加權集合覆蓋，每個集合類被賦予不同的權值，從而由權值決定最終的選擇。
對於完全集合覆蓋問題的決定版本是NPC（non-deterministic polynomial complete）的，而最佳化版本是NP-hard的
研究
給定兩個集合E和S，元素的集合E和E的子集的集合S，求出S的子集C，使得C中所有集合的並等於E，同時使得|C|最小。這就是經典的集合覆蓋問題(SCP)。它是NP-hard類的最最佳化組合問題。對於NP-HARD類的問題，在P≠NP的假設下，是不存在多項式時間算法的，只能設計求解他們的近似算法或近似方案，或者對於問題條件進行限制使得限制後的子問題是一個非NP-HARD類的問題。集合覆蓋問題在實際套用中有好多變型。若對於任意的s∈S有一個權重w(s)，並且同樣求c，使得sum from s∈C w(s)最小。問題就成為了帶有權重的集合覆蓋問題。若對於任意s∈S有一個限制正整數k(s)，使得在s中的至多覆蓋k(s)個元素，問題就成為帶容量限制的集合覆蓋問題(CSCP)，可以看出帶權重或帶容量限制的集合覆蓋問題至少和集合覆蓋問題一樣難。Lang和Yannakanis證明了集合覆蓋問題不存在c(lnn)，c<1/4的近似算法，除非NP(?)...
