最小圓覆蓋算法

最小圓覆蓋是數學中的一個算法問題，研究如何尋找能夠覆蓋平面上一群點的最小圓。這個問題在一般的維空間中的推廣是最小包圍球的問題，即尋找能覆蓋維空間中某個點集的最小球。最小圓覆蓋問題最早由十九世紀的英國數學家詹姆斯·約瑟夫·西爾維斯特在1857年提出。 最小圓覆蓋也是運籌學中設施選址問題的一種。廣義的設施選址問題研究的是當已知一些目標點（倉庫、銷售終端、供應商等等）的位置時，求滿足與這些目標點的距離相關的點的某些極值。最小圓覆蓋可以看作是研究“到一些點的距離之最大值最小的點”的問題。現有的算法可以線上性時間內計算最小圓覆蓋或最小包圍球的問題。

算法描述

尋找最小覆蓋圓的大部分幾何方法都是尋找給定點集中經過最小覆蓋圓的那些點。這是基於以下兩個事實：

最小覆蓋圓是唯一存在的。

給定的點集中，最多有三個點在最小覆蓋圓上。如果有三個點在最小覆蓋圓上，那么最小覆蓋圓就是這三點的外接圓；如果只有兩個點在最小覆蓋圓上，那么最小覆蓋圓就是以這兩點之間的直線段為直徑的圓。

1.

最小覆蓋圓是唯一存在的。

2.

給定的點集中，最多有三個點在最小覆蓋圓上。如果有三個點在最小覆蓋圓上，那么最小覆蓋圓就是這三點的外接圓；如果只有兩個點在最小覆蓋圓上，那么最小覆蓋圓就是以這兩點之間的直線段為直徑的圓。

線性時間解決方案

正如Nimrod Megiddo所示，最小包圍圓可以線上性時間內找到，並且相同的線性時間界限也適用於任何常數維的歐幾里德空間中的最小包圍球。

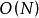最小圓覆蓋算法

Emo Welzl 基於Raimund Seidel的線性規划算法，提出了一種在預期 時間內運行的最小覆蓋圓問題的簡單隨機算法。 該算法如下所示。

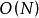最小圓覆蓋算法

最小圓覆蓋算法

隨後，最小圓問題被包含在一類普通的LP類型問題中，這些問題可以通過像Welzl基於線性規劃的算法來解決。 作為該類成員的結果，表明在 時間界限中對常數因子的維度的依賴性，這是Seidel方法的因子，可以減少到亞指數，但仍然只保持對 的線性依賴。

Welzl的算法

該算法是遞歸的，並且將兩個（有限的）點P和R作為參數;它計算P和R聯合的最小包圍圓，只要R的每個點都是最終最小包圍圓的邊界點之一。因此，原始的最小包圍圓問題可以通過調用算法來解決，其中P等於要封閉的點集合，R等於空集合;當算法遞歸調用自身時，它將放大傳遞給遞歸調用的集合R，直到它包含圓的所有邊界點。
該算法以隨機順序處理P的點，保持處理點的集合S和包含並集S∪R的最小圓D.在每一步，它測試下一個要處理的點p是否是在D;如果不是，該算法用集合S和R∪p上的算法的遞歸調用的結果替換D.無論圓是否被替換，p都被包括在集合S中。因此，處理每個點包括在恆定時間內測試該點是否屬於單個圓並且可能執行對算法的遞歸調用。可以看出，總時間是線性的。

其它算法

在Megiddo的結果顯示最小圓問題可以線上性時間內解決之前，文獻中出現了幾種更高複雜度的算法。一個樸素的算法通過測試由所有對和三元組確定的圓來解決時間O（n4）中的問題。

Chrystal和Peirce算法套用局部最佳化策略，該策略在包圍圓的邊界上保持兩個點並反覆收縮圓，替換該對邊界點，直到找到最佳圓。 Chakraborty和Chaudhuri [9]提出了一種線性時間方法，用於在該圓上選擇合適的初始圓和一對邊界點。算法的每個步驟包括作為兩個邊界點之一的凸包的新頂點，因此如果船體具有h個頂點，則該方法可以實現為在時間O（nh）中運行。

Elzinga和Hearn [10]描述了一種算法，該算法為點的子集保持覆蓋圓。在每個步驟中，當前球體未覆蓋的點用於查找覆蓋新的點子集的較大球體，包括找到的點。儘管其最差的運行時間是O（h3n），但作者報告說它在實驗中以線性時間運行。 Drezner和Shelah分析了該方法的複雜性。Fortran和C代碼均可從Hearn，Vijay&Nickel（1995）獲得。

最小的球體問題可以表示為由具有凸二次目標函式的線性約束系統定義的二次程式[1]。因此，任何可行的方向算法都可以解決問題。Hearn和Vijay證明Jacobsen選擇的可行方向方法等同於Chrystal-Peirce算法。

這個二次規劃的對偶也可以明確地表達出來; Lawson 的算法可以用這種方式描述為原始對偶算法。

Shamos和Hoey基於觀察得到了問題的O（n log n）時間算法，即最小包圍圓的中心必須是輸入點集的最遠點Voronoi圖的頂點。