基本介紹
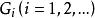 裝填問題
裝填問題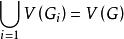 裝填問題
裝填問題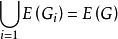 裝填問題
裝填問題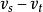 裝填問題
裝填問題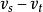 裝填問題
裝填問題圖論中有兩類相互有一定聯繫然而又是性質不同的問題,一類是研究用某種類型的子圖去覆蓋圖G的點集或邊集(即,或),這就是所謂覆蓋問題。例如正常邊染色是用邊不交的邊無關集覆蓋E(G);團覆蓋集是用團去覆蓋V(G)等等。一般說來,我們希望用最少個數的子圖去完成覆蓋,這就是最小覆蓋問題。另一類問題是研究從給定圖中,能取出多少個不交的某類子圖,或者反其意而說成是可以往給定圖中裝填多少個不交的某類子圖,這就是 裝填問題。一般說來,我們希望裝填的子圖個數儘可能地多,這就是 最大裝填問題。例如有向圖中弧形式的Menger定理所研究的是往D中裝填弧不交的()路。Menger定理是以最大最小定理的形式研究了能裝填k個弧不交的()路的充分必要條件 。
相關定理
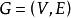 裝填問題
裝填問題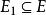 裝填問題
裝填問題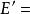 裝填問題
裝填問題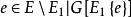 裝填問題
裝填問題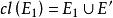 裝填問題
裝填問題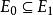 裝填問題
裝填問題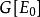 裝填問題
裝填問題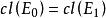 裝填問題
裝填問題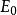 裝填問題
裝填問題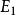 裝填問題
裝填問題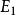 裝填問題
裝填問題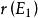 裝填問題
裝填問題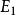 裝填問題
裝填問題給圖,對任意的,記{含過e的圈},定義稱為E-的閉集。一個子集,若不含圈,且,則稱為的一個基集。不難證明,的任何兩個基集,總包含相同個數的邊,定義為的基集所含的邊數。
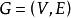 裝填問題
裝填問題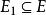 裝填問題
裝填問題定理1(Tutte,Nash-Williams,1961)中含有k個邊不交的支撐樹的充分必要條件是對任何,
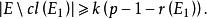 裝填問題
裝填問題定理1可以寫成另一種形式。
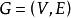 裝填問題
裝填問題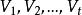 裝填問題
裝填問題定理1' 圖有k個邊不交的支撐樹,若且唯若對V的任意剖分,有
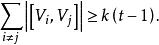 裝填問題
裝填問題需要指出的是定理1(1')對多重圖也是成立的,利用定理1,我們可以得到覆蓋邊集合所需要的森林的最小個數(記之為a(G),稱為圖G的蔭度) 。
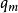 裝填問題
裝填問題定理2 令G是非平凡的多重圖,是G中m階子圖的最大邊數,令
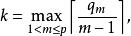 裝填問題
裝填問題則
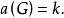 裝填問題
裝填問題
