統計量
一維資料的集中趨勢可能有以下數種統計方法。在某些情況下,經轉型(data transformation)後的資料才採用以下的方法。
算數平均數
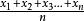 集中趨勢量數
集中趨勢量數觀測值的總和除以觀測值的個數,即 。常簡稱為平均數,也往往是背後機率分布的期望值之不偏估計。
中位數
將所有觀測值按大小排序後在順序上居中的數值。
眾數
出現最多次的觀測值。
幾何平均數
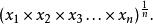 集中趨勢量數
集中趨勢量數觀測值的乘積之觀測值個數方根,即
調和平均數
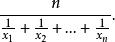 集中趨勢量數
集中趨勢量數觀測值個數除以觀測值倒數的總和,即
加權平均數
考慮不同群資料貢獻程度不同時的算數平均數。
截尾平均數(truncated mean)
忽略特定比例或特定數值之外的極端值後所得的平均數。例如,四分平均數(interquartile mean)正是忽略25%前及75%後的資料後所得的算數平均數。
全距中點(midrange)
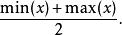 集中趨勢量數
集中趨勢量數最大值與最小值的算數平均數,即
中樞紐(midhinge)
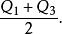 集中趨勢量數
集中趨勢量數第一四分位數與第三四分位數的算數平均數,即
三均值(trimean)
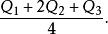 集中趨勢量數
集中趨勢量數考慮三個四分位數的加權平均數,即
極端值調整平均數(winsorized mean)
 集中趨勢量數
集中趨勢量數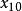 集中趨勢量數
集中趨勢量數以最接近的觀測值取代特定比例的極端值後取得的算數平均數。舉例來說,考慮10個觀測值(由小到大排列為 至 )的情況下,10%的極端值調整平均數為
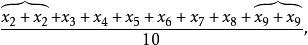 集中趨勢量數
集中趨勢量數 集中趨勢量數
集中趨勢量數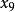 集中趨勢量數
集中趨勢量數 集中趨勢量數
集中趨勢量數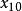 集中趨勢量數
集中趨勢量數其中分別以 和 取代了 和 。
以上的統計量在多維變數中仍可單獨地被套用在各個維度上進行,但並不能保證在轉軸後仍維持一致的結果。
數的關係
在左右對稱的機率分布中,不同的集中趨勢統計量有相同結果,但在偏度遠離0時則可能不一致。在單峰型的機率分布(unimodal probability distribution)中,平均數( μ)、中位數( ν)與眾數( θ)的關係如下:
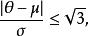 集中趨勢量數
集中趨勢量數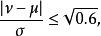 集中趨勢量數
集中趨勢量數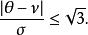 集中趨勢量數
集中趨勢量數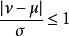 集中趨勢量數
集中趨勢量數其中 σ為標準偏差。至於任一機率分布, 。
