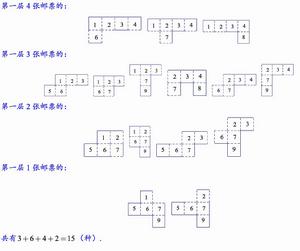
基本思路
0-1規劃是一種特殊的純整數規劃。求解0-1規劃的隱枚舉法不需要用單純形方法求解線性規劃問題。它的基本思路時從所有變數等於零出發,依次指定一些變數為1,直至得到一個可行解,並將它作為目前最好的可行解。此後,依次檢查變數等於0或1的某些組合,以便使目前最好的可行解不斷加以改進,最終獲得最優解。隱枚舉法不同於窮舉法,它不需要將所有可行的變數一一列舉。它通過分析、判斷派出了許多變數組合作為最優解的可能性。也就是說,它們被隱含枚舉,故此得名。
隱枚舉法也可以用於解最小化問題。如果問題的目標函式為最小化,可先讓所有的0-1變數取1,然後逐一檢查每一個變數取0的情況,能使目標函式進一步減小並使每一約束保持可行者為可行解。
過渡性隱枚舉法
用隱枚舉法解0-1規劃,其基本思想是:從所有變數等於零出發,依次指定一些變數為1,直至得到一個可行解,並將它作為目前最好的可行解。並引入一個過渡性條件作為新的約束條件加入到原問題中去,以排除一批相對較劣的可行解,然後再依次檢查變數取0或1的各種組合,看是否能對前面所得到的最好可行解有所改進,直到獲得最優解為止,這種方法稱為過渡性隱枚舉法。
步驟
隱枚舉法的解法如下:
第1步,化成0-1規劃的標準形式。
(1)目標函式化為求極小,約束條件均化為≥形式.這隻要對需要變換的約束式或目標函式乘以-1即可。
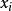 隱枚舉法
隱枚舉法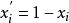 隱枚舉法
隱枚舉法(2)若目標函式中變數 的係數是負值,則通過 ,使係數化為正值。
(3)目標函式中,按變數係數從小到大排列,約束條件中的各項也按目標函式中變數的順序排列,不妨設重新排列後變數的順序為x1,x2……xn。
這就把原始問題化成了線性規劃的標準形式。
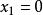 隱枚舉法
隱枚舉法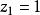 隱枚舉法
隱枚舉法第2步(分枝定界),首先令所有的變數均取值為0,求出目標函式值,並檢查變數的取值是否滿足約束條件,將此問題分成兩個子問題:一個分枝為 ,一個分枝為 ,其餘變數仍然取0,求出目標函式值,並檢查變數的取值是否滿足約束條件,按照下面原則決定是否繼續分枝:
(1)當分枝的子問題為可行解時,則該分枝即停止繼續分枝,並保留所有可行解中目標值最小的分枝,將可行解中邊界值(分支的最後一個目標函式)大的分枝去掉。
(2)不管是否為可行解,只要該分枝的邊界值大於保留下來的可行解的邊界值時,則該分枝停止分枝。
當分枝中某些變數的值已確定,而其他變數無論取什麼值,都至少有一個約束條件不被滿足時,則該分枝即停止分枝,否則繼續分枝,直到除了保留的分枝外,其餘分枝已全去掉,這時保留下來的可行解值即為所求問題的最優解。
原理
隱枚舉法從所有變數集等於零出發,然後,依次指定一些變數取值為1,直到獲得一個使目標函式下降(或上升)的可行解。於是可認為這個可行解是迄今為止最好的可行解。如此試探地選擇變數,用這種方法依次檢查變數集等於0或1的各種組合,並對可行解加以改進,直到獲得最優解。由於許多不可能得到較好可行解的變數組合併沒有被檢查,因而稱為隱枚舉法。隱枚舉法較顯枚舉法的好處是運算次數大大減少。
上述的隱枚舉計算方法僅僅能解0-1整數線性規劃問題,即對每個變數必須用0-1變數表示。
改進
在隱枚舉法的基礎上,又提出一種所謂的改進的隱枚舉法。這種方法的思想是,對於具備隱枚舉法條件的0-1規劃問題,一方面考慮,約束條件的係數,儘早去掉不滿足約束條件的各種變數取值的組合;另一方面又考慮目標函式值,儘早去掉不會使目標函式值比已知可行解目標函式值更小的各種變數取值的組合,使得被考慮的各種變數取值的情形大大減少,加快了計算的進程。