簡介
鐵木辛柯梁是20世紀早期由美籍俄裔科學家與工程師史蒂芬·鐵木辛柯提出並發展的力學模型。模型考慮了剪應力和轉動慣性,使其適於描述短梁、層合梁以及波長接近厚度的高頻激勵時梁的表現。結果方程有4階,但不同於一般的梁理論,如歐拉-伯努利梁理論,還有一個2階空間導數呈現。實際上,考慮了附加的變形機理有效地降低了梁的剛度,結果在一穩態載荷下撓度更大,在一組給定的邊界條件時預估固有頻率更低。後者在高頻即波長更短時效果更明顯,反向剪力距離縮短時也有同樣效果。
如果梁材料的剪下模量接近無窮,即此時梁為剪下剛體,並且忽略轉動慣性,則鐵木辛柯梁理論趨同於一般梁理論。
主要內容
鐵木辛柯梁(Timoshenko梁)就是能考慮剪下變形的梁。具體地說,它的位移和截面轉角是獨立插值的,而不是由位移的導數來求得。具對於梁的高度(或者直徑)較大,高跨比增加,必須考慮剪下變形和轉動慣量的梁相對的,不需要考慮的就是歐拉-伯努力梁。
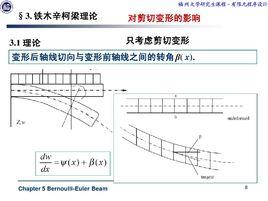
簡單地說,鐵木辛柯梁是考慮剪下的梁,歐拉梁就是材料力學裡講的梁,忽略剪下作用。
鐵木辛柯梁主要考慮剪下變形,而且位移和轉角是獨立插值的,不是通過位移導數求得。
歐拉梁基於平截面面假定,彎曲是主要變形,忽略剪下變形的影響,其計算公式通過平衡微分方程得到,而非變形協調方程。
套用
現今套用中梁理論主要有:
(1)精確的彈性方程
(2)Euler-Bernoulli梁理論
(3)Timoshenko梁理論。
彈性理論方法有一個主要的缺點是只能精確的求解極少問題(Coper,1968),因此它並不具有很好的吸引力。
Euler-Bernoulli梁理論(Shames and Dym,1985)認為橫截面在變形前和變形後都垂直於中心軸並不受任何應變(也就是說其構型仍無缺的)。換句話說,翹曲和橫向剪下變形的影響和橫向正應變非常小,所以可以忽略不計。這些假設對細長梁是有效的。無橫向剪下意味著橫截面的旋轉只由撓曲引起。對於厚梁,高頻模態的激勵,複合材料梁問題,橫向剪下不可以忽略。
將橫向剪下變形加入Euler-Bernoulli梁模型就得出Timoshenko梁理論(Timoshenko,1921,1922;Meirovitch,1967;Shames and Sym,1985)。在此理論中,為了簡化運動方程的導數,剪應變在一個給定橫截面上是常值。接著引入剪下校正因子來解釋這種簡化,其值取決於橫截面的形狀(Timoshenko,1921;Cowper,1966,1968)。在橫向剪下的存在下,橫截面的旋轉就由撓曲和橫向(平面外)剪變形引起。