定義
配對函式是雙射函式:
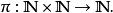 配對函式
配對函式康托爾配對函式
 康拖爾配對函式
康拖爾配對函式康托爾配對函式是配對函式:
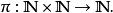 配對函式
配對函式定義為:
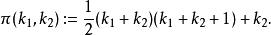 配對函式
配對函式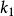 配對函式
配對函式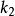 配對函式
配對函式 配對函式
配對函式在套用配對函式到和的時候,我們經常指示結果的數為
這個定義可以歸納一般化為 康托爾元組函式:
 配對函式
配對函式作為:
 配對函式
配對函式反轉康托爾配對功能
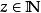 配對函式
配對函式讓是一個任意的自然數。證明存在的價值:
 配對函式
配對函式因此 π是可逆的。在計算中定義一些中間值是有幫助的:
 配對函式
配對函式 配對函式
配對函式 配對函式
配對函式其中t是w的三角形數。如果我們解二次方程:
 配對函式
配對函式得到:
 配對函式
配對函式當 t是非負實數時,這是一個嚴格遞增和連續的函式。
 配對函式
配對函式可以得到:
 配對函式
配對函式因此:
 配對函式
配對函式其中⌊⌋是高斯符號。可以得到:
 配對函式
配對函式 配對函式
配對函式 配對函式
配對函式 配對函式
配對函式
