背景
圖像邊緣包含了圖像最重要的信息。所謂邊緣一般是指圖像灰度變化率最大的集合， 所以邊緣廣泛存在於物體與背景之間、物體與物體之間、基元與基元之間。由於圖像邊緣包含了大量的圖像的重要信息，因此，圖像邊緣檢測成為圖像處理的一個重要環節。
目前國內外對圖像邊緣檢測有著比較廣泛的研究，經典的邊緣檢測運算元常藉助空域微分運算元進行，通過微分模板與圖像卷積完成。常見的邊緣運算元有 Roberts、Sobel、Prewitt和Krisch 等，其中 Sobel 運算元[1] 檢測速度快， 是實踐中最常用的運算元；但是 Sobel 運算元通過閾值對梯度場進切割得到圖像邊緣，閾值過大會造成邊緣的丟失，閾值過小又會造成一些非邊緣點當成邊緣點被分割出來進而形成偽邊緣。
近年來隨著數學理論和人工智慧的不斷發展，許許多多新的邊緣檢測方法被提出。基於小波變換的圖像邊緣檢測具有能避免噪聲干擾的特點，但會丟失一些弱邊緣；基於模糊理論的邊緣檢測算法具有較的抗噪能力， 但矩陣變換的運算較為複雜；基於蟻群算法的邊緣檢測對噪聲有良好的免疫作用，但會丟失一些邊緣信息。
傳統的圖像邊緣檢測運算元一般都只能得到多像素寬邊緣，這為後續的圖像處理帶來了一定困難。正由於邊緣細化算法較為重要，因此其一直以來都得到學者的關注，並已取得了一定的研究成果。現有的邊緣細化算法可粗略地分為兩大類：基於二值邊緣圖像的方法和基於數學形態學的方法。
細化方法
所謂細化，通常是把一個具有一定面積的區域用一條曲線來代表它。邊緣細化，即為把較粗的邊緣用一條較細的曲線來表示。
基於數學形態學
數學形態學細化算法的主要思想是源於擊中擊不中變換的形態學算法。在給定一系列具有一定形狀的結構元素後，順序循環地刪除滿足擊中變換的像素。
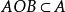邊緣細化所謂細化，就是尋找圖形、 筆劃的中軸線或骨架， 以其骨架取代該圖形或筆劃。 在遵循對圖像的細化要保持圖像連通性的最基本原則下，細化之後的圖形或筆劃的像素寬度為 1。 細化過程也就是對圖像逐層剝落的過程，隨著細化的進行，圖像有規律地縮小。 數學形態學基本運算中的薄化，即 AOB，可以使圖形按一定規律不斷縮小， 並始終保持 。
結構元素 B的選擇尤為重要，是影響細化質量的關鍵因素。 細化算法將不斷重複地剝離二值圖像的邊界像素。但是， 對於邊界像素的剝離應保持目標圖像紋線的連線性，方向性和特徵點不變，還應保持紋線的中心基本不變，最終使得變換圖像成為單像素寬的圖像骨架。
下面舉例說明：
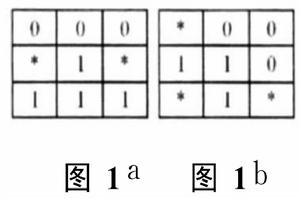
考慮以上因素，採用圖 1所示結構元素。其中，符號 “*”表示既可取灰度 1，又可取灰度 0的像素。然後將這兩種結構元素 (a)、(b)陸續旋轉 90°、180°和 270°，得出 6 種結構元素, 共有8種結構元素。這 8種結構元素分別對應著東、西、南、北及東北、西北、西南及東南8個方向上的邊界點。
邊緣細化結構元素確定後，利用形態學中的薄化運算對圖像進行細化。
基於二值邊緣圖像
圖像細化就是從原來的圖像中去掉一些點，但仍要保持目標區域的原來形狀。二值邊緣圖像細化即是判斷原邊緣上每一像素點是否應被剔除，以此來一層層剝離原邊緣最外層的偽邊緣。
以HSCP邊緣細化算法為例。
首先給出圖像中像素點 8 連通域示意圖，下圖所示。則HSCP 算法可簡述如下：
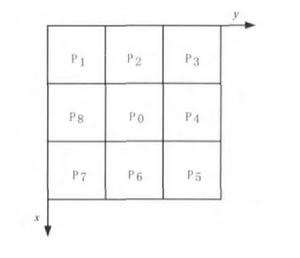8連通域示意圖
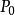邊緣細化Step1：針對所有的邊緣點 ，若滿足如下條件，則判斷其為待剔除點。
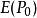邊緣細化
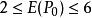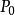邊緣細化 邊緣細化（1）其 8 連通域中的邊緣點數滿足:；
( 2)的 8 連通域包含且只包含一個 4 連通邊緣點。
Step2：遍歷所有的待剔除點， 若滿足如下條件之一，則保留，否則刪除。
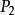邊緣細化
邊緣細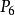化
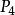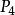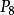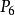邊緣細化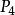 邊緣細化
邊緣細化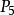 邊緣細化 邊緣細化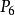
邊緣細化 邊緣細化（1），為邊緣點，但為待剔除點；
（2），為邊緣點，但為待剔除點；
（3），，均為待剔除點。
以上兩步操作構成一次疊代，不難發現，在每次疊代中需兩次循環遍歷，首先需遍歷全部邊緣點，判斷是否為待剔除點; 然後再次遍歷全部待剔除點，再次判斷這些點是否確實可剔除， 目的是防止過多地剔除邊緣細節， 保持原有邊緣的連續性。此算法計算量較大。
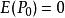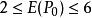邊緣細化 邊緣細化上述算法被指出具有兩個缺陷：
（1）保留了孤立的邊緣點。因為孤立點 8 鄰域內非零點的個數為 0，即， 而待剔除點必須滿足，所以孤立點未被剔除。
（2）運算量較大。採用兩層循環構成一次疊代，儘管每次疊代對象不盡相同，算法開銷依然較大
三個性質
一個性能良好的邊緣細化算法應該具有如下三個性質：
（1）單像素寬細化結果
理想的算法應該能給出單像素寬的細化結果。
（2）保持邊緣的原有信息
邊緣細化結果不能改變邊緣的原有信息，即邊緣的連通和走向趨勢， 因為這些信息是進行圖像理解、目標識別的重要依據。
（3）計算開銷小
能被實際廣泛運用的算法自然是計算開銷小 、執行效率高的方法
