達維多夫孤子
解釋
達維多夫孤子是量子準粒子較激勵沿著蛋白α螺旋自陷醯胺I.傳播它是達維多夫哈密頓的溶液。它被命名為蘇聯和烏克蘭物理學家亞歷山大·達維多夫。所述達維多夫模型描述與氫鍵即穩定α螺旋的蛋白質的醯胺I振動的相互作用。在α螺旋中的元激發是由對應於晶格的變形振湯的聲子,並且其描述了肽基團的內醯胺I激發激子給出。參照蛋白質的創建該達維多夫孤子的機構(極化子,激子)的α螺旋區域的原子結構可以描述如下:作為C振動能量= O伸縮(或醯胺I),其定位於所述振湯器α螺旋作用通過聲子耦合效應扭曲α螺旋的結構,而該螺旋失真再次起反應,通過聲子耦合到陷阱醯胺予振動能量並防止其擴散。這種效應被稱為自定位或自陷。[孤子其中能量是分布在一個方式保持螺旋對稱是動態不穩定,並且這種對稱孤子一旦形成迅速衰減它們傳播時。另一方面,非對稱孤子自發分解局部平移和螺旋對稱性具有最低的能量,並且是堅固的局部實體。
形式
達維多夫的哈密頓在形式上類似於弗羅利希 - 霍爾斯坦哈密頓電子與極化晶格的相互作用。因此,能源運營商的哈密頓H^是
 達維多夫孤子
達維多夫孤子哪裡是H^qp準粒子(激子)哈密爾頓,它描述了醯胺相鄰站點之間我激勵的議案;H^int是聲子哈密頓,它描述了晶格的振動;並且是相互作用哈密頓,它描述了醯胺I激勵與晶格的相互作用。
準粒子
準粒子(激子)哈密爾頓
準粒子(激子)哈密爾頓H^qp是:
 達維多夫孤子
達維多夫孤子 達維多夫孤子
達維多夫孤子 達維多夫孤子
達維多夫孤子 達維多夫孤子
達維多夫孤子 達維多夫孤子
達維多夫孤子 達維多夫孤子
達維多夫孤子 達維多夫孤子
達維多夫孤子其中索引計數(n=1,2,......n)沿著α螺旋脊的肽基團,該指數 計算每個α螺旋脊, J是I醯胺振動(CO伸縮)的能量, J是一個特定的醯胺I之間的偶極 - 偶極耦合的能量鍵和那些前方並沿同一脊柱後面, J是一個特定的醯胺I鍵和那些相鄰棘在蛋白α螺旋的相同單元電池之間的偶極 - 偶極耦合的能量, 和 並分別為玻色子的產生和湮滅操作者對一個準粒子在肽基。
聲子哈密頓
 達維多夫孤子
達維多夫孤子聲子哈密頓 是:
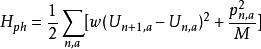 達維多夫孤子
達維多夫孤子 達維多夫孤子
達維多夫孤子 達維多夫孤子
達維多夫孤子 達維多夫孤子
達維多夫孤子其中 是從肽基的平衡位置的位移操作者, 是該肽基的動量算符,M是每種肽基團的質量,和 N m是晶格的有效彈性係數(一氫的彈簧常數債券)。
相互作用哈密頓
 達維多夫孤子
達維多夫孤子最後,相互作用哈密頓 是:
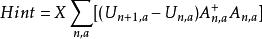 達維多夫孤子
達維多夫孤子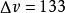 達維多夫孤子
達維多夫孤子其中PN是從準粒子(激子)之間的耦合所產生的非諧參數和晶格位移(聲子)和參數化的激子 - 聲子相互作用的強度。此參數為α螺旋的值已經通過理論計算吸收線的形狀與實驗測得的那些進行比較得到確定。
被用來分析達維多夫的孤子的數學技術類似於一些已經開發了在極化子理論。在這方面,達維多夫的孤子對應於極化子是(Ⅰ)大,從而連續極限近似是合理的,(Ⅱ)聲,因為自定位產生於與晶格的聲波波型的相互作用,和(iii)弱耦合,因為與聲子頻寬相比的非調諧能量是小的。
在達維多夫孤子是量子準粒子,它服從海森堡的不確定性原理。因此,這並不強加平移不變性任何模型由施工有缺陷的。[5]假設該達維多夫孤子被定位到5匝的α螺旋的結果中的不確定性顯著在孤子米/秒的速度,這一事實是遮蔽如果一個模型達維多夫孤子作為一個經典的對象。
有朝向達維多夫模型三種可能的基本方法:(i)該量子理論,其中兩個I醯胺振動(激子)和晶格點的運動(聲子)的機械處理量子; (ii)該混合量子經典理論,其中醯胺I振動被機械處理量子但晶格是經典;和(iii)的經典理論,在其中醯胺I和晶格兩個運動是古典的處理。
