過濾的水頭損失
預測水通過濾層所產生的水頭損失,是過濾水力學的一項最基本內容,也是過濾理論的一個部分。不幸的是,由於缺乏濾層孔隙度在過濾過程中隨著時間以及高度變化的可靠理論,目前只能夠計算過濾剛開始,濾層處於清潔狀態下的水頭損失。下面為水頭損失公式的推導,下圖表示出推導的有關因素。
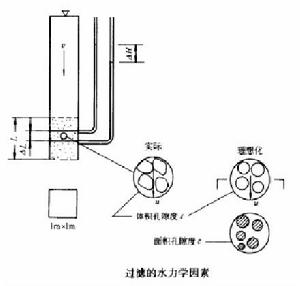 過濾的水力學因素
過濾的水力學因素 過濾水頭
過濾水頭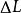 過濾水頭
過濾水頭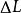 過濾水頭
過濾水頭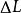 過濾水頭
過濾水頭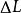 過濾水頭
過濾水頭 過濾水頭
過濾水頭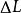 過濾水頭
過濾水頭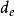 過濾水頭
過濾水頭 過濾水頭
過濾水頭 過濾水頭
過濾水頭 過濾水頭
過濾水頭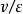 過濾水頭
過濾水頭上圖表示推導水頭損失公式有關的水力學因素,具體條件是:面積為(1m²),濾層厚度為L(m),濾速為 (m/s)。先取L中的一段 來分析,並作下列假定:(1)在 厚度內的濾料是均質的,當進行較精確的計算時, 必須取得很薄,但在計算要求不嚴格時,甚至可以把整個濾層取為 ;(2)把孔隙度為 的 厚度濾料理想化為同樣孔隙度的球形濾料,並用這些大小不等球形的當量粒徑 來代表它們的大小。濾料理想化後的濾層的橫斷面孔隙度仍為 ,因為只有這樣,才能得到一個體積孔隙度仍為 的濾層。水通過斷面的真實速度 因之等於 。
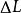 過濾水頭
過濾水頭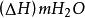 過濾水頭
過濾水頭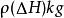 過濾水頭
過濾水頭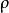 過濾水頭
過濾水頭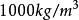 過濾水頭
過濾水頭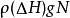 過濾水頭
過濾水頭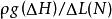 過濾水頭
過濾水頭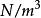 過濾水頭
過濾水頭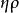 過濾水頭
過濾水頭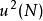 過濾水頭
過濾水頭如圖中所示, 濾層的水頭損失為 ,相當於 重, 為水的密度( ),相當於 ,因此得在每平方米濾料上每米濾料所產生的阻力,即單位體積濾料所產生的阻力為 ,其單位為 。另一方面,水流過固體所產生的阻力可表示為 (固體面積) ,單位體積濾料所產生的阻力可表示為:
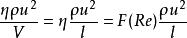 過濾水頭
過濾水頭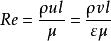 過濾水頭
過濾水頭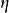 過濾水頭
過濾水頭式中, ——阻力係數,為Re的函式;
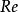 過濾水頭
過濾水頭——過濾的水流雷諾數;
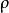 過濾水頭
過濾水頭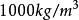 過濾水頭
過濾水頭——水的密度, ;
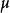 過濾水頭
過濾水頭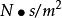 過濾水頭
過濾水頭——水的動力粘度, ;
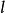 過濾水頭
過濾水頭——計算Re所用的水流特徵長度。
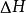 過濾水頭
過濾水頭把水頭損失 表示阻力的關係和上式(阻力公式)聯繫起來,得出下面的過濾阻力的基本方程式:
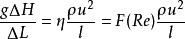 過濾水頭
過濾水頭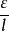 過濾水頭
過濾水頭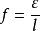 過濾水頭
過濾水頭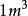 過濾水頭
過濾水頭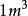 過濾水頭
過濾水頭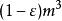 過濾水頭
過濾水頭在Re的表達式中, 可以按量綱解釋合併成另一個具有物理意義的參數f,即 。其代表了 濾層中濾料所具有的表面積,這是與水接觸的面積,是產生阻力的來源,故具有重要的物理意義。 濾層中濾料的體積為 ,假定濾料皆為直徑為d的球形時,則f可表示為:
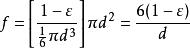 過濾水頭
過濾水頭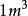 過濾水頭
過濾水頭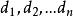 過濾水頭
過濾水頭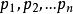 過濾水頭
過濾水頭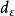 過濾水頭
過濾水頭 過濾水頭
過濾水頭方括弧內為 濾層中濾料的顆粒數。當濾料包括粒徑為 的顆粒,並在濾料中分別占百分數 時,則由上式定義當量粒徑 ,再把濾料的形狀係數 考慮在內,則特徵長度與當量粒徑有下列關係:
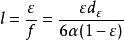 過濾水頭
過濾水頭再把上式代入上面雷諾數的表達式中,可得:
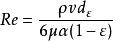 過濾水頭
過濾水頭根據清潔砂粒的試驗資料,按上面推導出的公式得計算結果,可以把阻力係數和雷諾數的對數坐標圖繪出,如下圖所示。
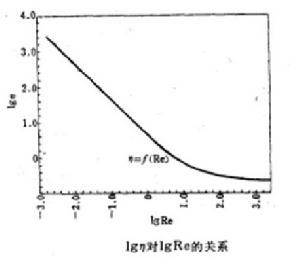 阻力係數和雷諾數的對數坐標圖
阻力係數和雷諾數的對數坐標圖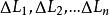 過濾水頭
過濾水頭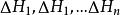 過濾水頭
過濾水頭經過分析,如果把整個濾層L分成 等濾層,相應的水頭損失為 ,則總的水頭損失H為:
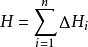 過濾水頭
過濾水頭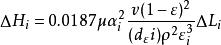 過濾水頭
過濾水頭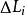 過濾水頭
過濾水頭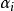 過濾水頭
過濾水頭 過濾水頭
過濾水頭對每一 來說, 和 值應相等。
過濾水頭損失分析
現以下向流恆速普通快濾池為例,簡要分析濾池的水頭損失。假設在整個過濾周期內,濾池的水位和濾速都保持不變,那么如果測得濾池進水、出水以及出水閥後的水頭,就能得出濾池各部位水頭損失的變化情況,如下圖所示。
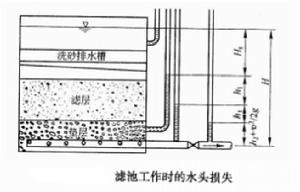 濾池工作時的水頭損失
濾池工作時的水頭損失 過濾水頭
過濾水頭 過濾水頭
過濾水頭 過濾水頭
過濾水頭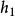 過濾水頭
過濾水頭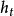 過濾水頭
過濾水頭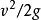 過濾水頭
過濾水頭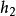 過濾水頭
過濾水頭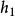 過濾水頭
過濾水頭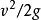 過濾水頭
過濾水頭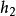 過濾水頭
過濾水頭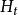 過濾水頭
過濾水頭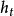 過濾水頭
過濾水頭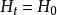 過濾水頭
過濾水頭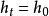 過濾水頭
過濾水頭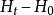 過濾水頭
過濾水頭 過濾水頭
過濾水頭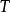 過濾水頭
過濾水頭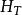 過濾水頭
過濾水頭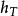 過濾水頭
過濾水頭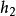 過濾水頭
過濾水頭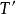 過濾水頭
過濾水頭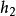 過濾水頭
過濾水頭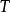 過濾水頭
過濾水頭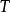 過濾水頭
過濾水頭在過濾開始的 時刻,濾池的總水頭 可分解為如下五部分:濾層的水頭損失 ,墊層和配水系統的水頭損失 ,流量控制閥(出水閥)的水頭損失 。出水管的流速水頭 和剩餘水頭 。就一定的濾池而言, 、 和 可認為是定值,變化的只是 和 。開始過濾時,乾淨濾層的水頭損失最小( ),而出水閥開啟度最小,水頭損失最大( )。根據測試資料,濾層的水頭損失增量( )隨過濾時間 的延長呈直線變化(見下圖)。為了補償此水頭損失,出水閥的開啟度必須隨著增大,也即水頭損失應相應地減少,減少值應等於濾層的水頭損失增加值。當過濾時間為 時,濾層水頭損失達到 ,此時出水閥全開,其阻力損失達到最小值 。如果繼續進行過濾,則剩餘水頭 就要被動用。而當過濾時間達到 時, 被消耗完,以致濾池不再出水。在實際操作中,過濾時間達到 時,就停止過濾而進行反洗,時間 即為濾池的過濾周期。
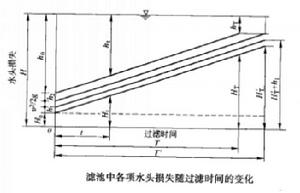 濾池中各項水頭損失隨過濾時間的變化
濾池中各項水頭損失隨過濾時間的變化濾池的反洗
濾池多採用水力逆流沖洗,以清除污物。沉積於濾層內的污物是靠上升的反洗水流的剪力以及濾料顆粒之間的碰撞和摩擦而剝落下來,並隨水流沖走的。因此。反洗強度要足以使濾料懸浮起來,即必須造成濾層的膨脹。但反洗強度過大,濾層膨脹過高,則因減小了單位體積流化床內的濾料顆粒數而使碰撞機會減少,反而使反洗效果變差;此外,還會造成濾料流失和沖洗水的浪費,以及衝起墊層。因此,確定適宜的反洗強度和濾層膨脹率是十分重要的。
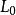 過濾水頭
過濾水頭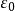 過濾水頭
過濾水頭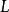 過濾水頭
過濾水頭 過濾水頭
過濾水頭 過濾水頭
過濾水頭設靜止濾層的厚度為 ,空隙率為 ,反衝洗時流化床高度為 ,空隙率為 ,則濾層膨脹率 可用下式表示:
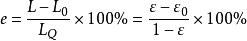 過濾水頭
過濾水頭反洗時單位濾池面積上通過的反洗水流量,稱為反洗強度,以q表示,單位常用L/(m²·s)。據試驗,濾層膨脹率與反洗強度的關係如下圖所示。
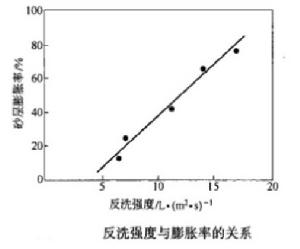 反洗強度與膨脹率的關係
反洗強度與膨脹率的關係適宜的反洗強度依濾料級配、相對密度和水溫而異。濾料粒徑相同時,相對密度大的要求較大的反洗強度;相對密度相同時,粒徑較大的要求反洗強度也大。此外,作用在流化床中濾料顆粒上的拖曳力與水的動力黏度成正比。水溫高時水的黏度小,不利於污物的剝離,因此要有較大的反洗強度,其值可按下式修正:
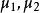 過濾水頭
過濾水頭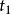 過濾水頭
過濾水頭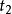 過濾水頭
過濾水頭式中, ——分別是溫度為 和 時水的動力粘度;
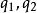 過濾水頭
過濾水頭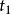 過濾水頭
過濾水頭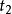 過濾水頭
過濾水頭——分別是溫度為 和 時的反洗強度。

