速度-距離關係
正文
1929年哈勃發現星系的退行速度與距離成正比,這是速度與距離之間最簡單的(線性的)關係。在天文學上,星系的速度和距離是不能直接測定的,可以直接測定的是星系的紅移和視星等(見星等)。哈勃把觀測到的紅移歸因於都卜勒效應,從而得到退行速度,並根據星系中造父變星的周光關係定出了星系的距離。假設紅移z與距離D之間的關係為:z=bDα, (1)
式中a、b為常數;並假設所有星系的絕對星等相同,則根據絕對星等與距離之間的定義關係可得: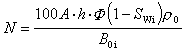 。(2)
。(2)
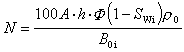
1929年哈勃發現星系的退行速度與距離成正比,這是速度與距離之間最簡單的(線性的)關係。 (1)式中a、b為常數;並假設所有星系的絕對星等相同,則根據絕對星等與距離之間的定義關係可得: 。 只有當這個斜率為0.2時才對應於紅移與距離之間的線性關係。
z=bDα, (1)
式中a、b為常數;並假設所有星系的絕對星等相同,則根據絕對星等與距離之間的定義關係可得: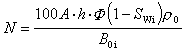 。(2)
。(2)
1929年哈勃發現星系的退行速度與距離成正比,這是速度與距離之間最簡單的(線性的)關係。 式中a、b為常數;並假設所有星系的絕對星等相同,則根據絕對星等...
測量天體距離的最經典的方法是三角視差法,此外還有許多方法。每種方法都有一定的適用範圍。
介紹 測量方法(太陽系內的天體 ) 測量方法(太陽系外的遠天體)速度素質是指人體快速運動的能力。快速運動反映著機體運動的加速度和最大速度的能力。反應速度是指人體對各種信號刺激(聲、光、觸等)快速應答的能力。動作速度是...
反應速度 動作速度 移動速度 速度素質經常使用ADSL的用戶,你知道ADSL的真正速度嗎?帶著這個疑問我們將問題一步一步展開。
介紹 說明好吃的料理=50%高貴的食材+50%精湛的手藝??唯有以真心的溫暖為佐料,佐以陷入熱戀的心情,在人與人的冷漠之間,才能營造出一次次100%令人溫暖又幸福...
簡介 內容簡介 分集介紹 角色介紹 幕後這個關係可測定恆星的距離。常用的星際吸收線是最強的電離鈣的K線和中性鈉...的距離。 星群視差法 移動星團的成員星都具有相同的空間速度。由於透視...)對恆星的視向速度有影響。這種影響的大小與星群離太陽的距離遠近有關,因此可從視...
天體的距離 正文 配圖 相關連線計程車幾何或曼哈頓距離(Manhattan Distance)是由十九世紀的赫爾曼·閔可夫斯基所創辭彙 ,是種使用在幾何度量空間的幾何學用語,用以標明兩...
簡介 數學性質 棋盤上的距離計量起飛距離,是指完成起飛過程飛機經過的水平距離。噴氣運輸機的起飛距離有兩種:全部發動機工作的正常起飛距離;一台發動機停車情況下的繼續起飛距離。為了檢査實際...
定義 起飛速度 起飛類型《速度管理》手冊的背景 速度管理的目標 速度管理項目的評估
圖書信息 內容簡介 圖書目錄