基本介紹
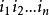 逆序數列
逆序數列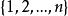 逆序數列
逆序數列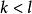 逆序數列
逆序數列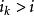 逆序數列
逆序數列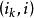 逆序數列
逆序數列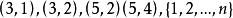 逆序數列
逆序數列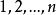 逆序數列
逆序數列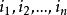 逆序數列
逆序數列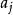 逆序數列
逆序數列 逆序數列
逆序數列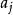 逆序數列
逆序數列 逆序數列
逆序數列 逆序數列
逆序數列 逆序數列
逆序數列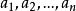 逆序數列
逆序數列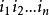 逆序數列
逆序數列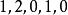 逆序數列
逆序數列利用逆序來描述排列的方法是M.Hall,Jr發現的。逆序的概念是一個舊概念,它在矩陣的行列式理論中起著重要作用。令是集合的一個排列。如果而,稱為一個 逆序。於是,逆序對應一對數,它們在排列中失去自然次序。例如,排列31524中有4 個逆序,即的唯一沒有逆序的排列是。對於排列,我們令表示第二個分量為的逆序個數。換句話說,等於排列中先於且又大於的那些整數的個數。它度量的失序有多少。數列稱為排列的逆序數列。上例給出的數列的逆序數列是。
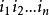 逆序數列
逆序數列排列的逆序數列必須滿足條件
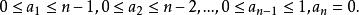 逆序數列
逆序數列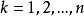 逆序數列
逆序數列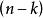 逆序數列
逆序數列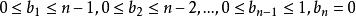 逆序數列
逆序數列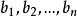 逆序數列
逆序數列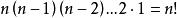 逆序數列
逆序數列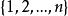 逆序數列
逆序數列這是顯然的,因為對每一個,在集合中都有個整數大於k。利用乘法原理,可知滿足的整數的個數等於。這些數列中每一個都唯一地對應的一個排列 。
定理構造方法
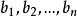 逆序數列
逆序數列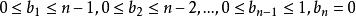 逆序數列
逆序數列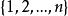 逆序數列
逆序數列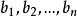 逆序數列
逆序數列定理1 設是整數數列且,則存在的唯一排列,其逆序數列是。
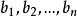 逆序數列
逆序數列證明:我們介紹一種方法,可用來唯一地構造其逆序數列為的一個數列。
 逆序數列
逆序數列 逆序數列
逆序數列:寫 出。
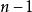 逆序數列
逆序數列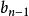 逆序數列
逆序數列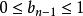 逆序數列
逆序數列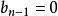 逆序數列
逆序數列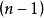 逆序數列
逆序數列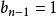 逆序數列
逆序數列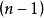 逆序數列
逆序數列:考察:。已知,如果,,則必在n的前面。如果,則必在n的後面。
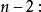 逆序數列
逆序數列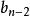 逆序數列
逆序數列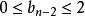 逆序數列
逆序數列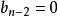 逆序數列
逆序數列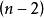 逆序數列
逆序數列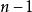 逆序數列
逆序數列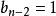 逆序數列
逆序數列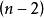 逆序數列
逆序數列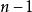 逆序數列
逆序數列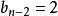 逆序數列
逆序數列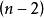 逆序數列
逆序數列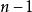 逆序數列
逆序數列考察。已知。如果,則必在由步得到的兩個數之前,如果,,則必在由步得到的兩個數之間。如果,,則必在由步得到的兩個數之後。
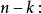 逆序數列
逆序數列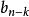 逆序數列
逆序數列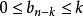 逆序數列
逆序數列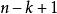 逆序數列
逆序數列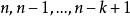 逆序數列
逆序數列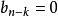 逆序數列
逆序數列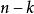 逆序數列
逆序數列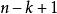 逆序數列
逆序數列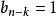 逆序數列
逆序數列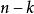 逆序數列
逆序數列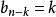 逆序數列
逆序數列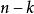 逆序數列
逆序數列(一般步)考察。已知,在由n到的各步中,k個數已按要求的次序放好。如果,則必在由步得到的所有數之前。如果,則必在頭兩個數之間。...如果,則必在所有數之後。
...
1:...
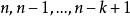 逆序數列
逆序數列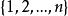 逆序數列
逆序數列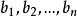 逆序數列
逆序數列作完諸步之後,就唯一確定了的排列,其逆序數列是。
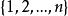 逆序數列
逆序數列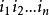 逆序數列
逆序數列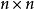 逆序數列
逆序數列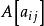 逆序數列
逆序數列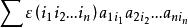 逆序數列
逆序數列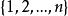 逆序數列
逆序數列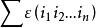 逆序數列
逆序數列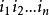 逆序數列
逆序數列習慣上,根據的排列的逆序個數是偶數還是奇數,稱它為 偶排列或 奇排列。排列的符號則根據它是否為偶或奇定義為+1或-1。在矩陣的行列式理論中,排列符號的概念是重要的,這裡階矩陣的行列式定義為。這裡求和是指對的所有排列求和,為的符號。
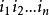 逆序數列
逆序數列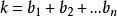 逆序數列
逆序數列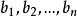 逆序數列
逆序數列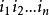 逆序數列
逆序數列 逆序數列
逆序數列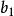 逆序數列
逆序數列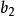 逆序數列
逆序數列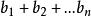 逆序數列
逆序數列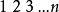 逆序數列
逆序數列若排列具有逆序個數為的逆序數列則可以相繼經過k次交換相鄰兩數得到。我們首先把1逐次與個在它左邊的數進行交換。然後把2逐次與個在它左邊的大於2的數交換,等等。用這種方法經次交換後,我們得到。
例題解析
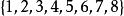 逆序數列
逆序數列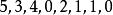 逆序數列
逆序數列試確定的排列,使其逆序數列為,對於給定的逆序數列,按照定理證明中的步驟,得到下面的結果:
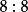 逆序數列
逆序數列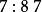 逆序數列
逆序數列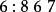 逆序數列
逆序數列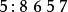 逆序數列
逆序數列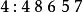 逆序數列
逆序數列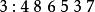 逆序數列
逆序數列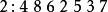 逆序數列
逆序數列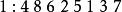 逆序數列
逆序數列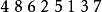 逆序數列
逆序數列於是,所求排列為。

