定義
若一n行n列的複數矩陣 U滿足
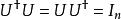 么正矩陣
么正矩陣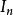 么正矩陣
么正矩陣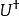 么正矩陣
么正矩陣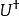 么正矩陣
么正矩陣其中為n階單位矩陣,為 U的共軛轉置,則 U稱為 酉矩陣(又譯作 么正矩陣、 么正矩陣。英文:Unitary Matrix, Unitary是 歸一或 單位的意思)。即,矩陣 U為酉矩陣,若且唯若其共軛轉置為其逆矩陣:
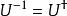 么正矩陣
么正矩陣若酉矩陣的元素都是實數,其即為正交矩陣。與正交矩陣 G不會改變兩個實向量的內積類似,
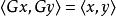 么正矩陣
么正矩陣酉矩陣 U不改變兩個復向量的內積:
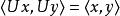 么正矩陣
么正矩陣若U為n階方陣,則下列條件等價:
(1)U是酉矩陣
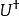 么正矩陣
么正矩陣(2)是酉矩陣
(3)U的列向量構成內積空間 C上的一組標準正交基
(4)U的行向量構成內積空間 C上的一組標準正交基
酉矩陣的特徵值都是模為1的複數,即分布在複平面的單位圓上,因此酉矩陣行列式的值為±1。
酉矩陣是正規矩陣,由譜定理知,酉矩陣 U可被分解為
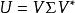 么正矩陣
么正矩陣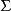 么正矩陣
么正矩陣其中 V是酉矩陣,是主對角線上元素絕對值為1的對角陣。
對任意 n,所有n階酉矩陣的集合關於矩陣乘法構成一個群。
性質
U可逆;
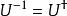 么正矩陣
么正矩陣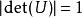 么正矩陣
么正矩陣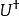 么正矩陣
么正矩陣是酉矩陣
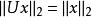 么正矩陣
么正矩陣參見
•埃爾米特矩陣
•辛矩陣
•酉群
•酉運算元
•矩陣分解